Système
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
misslolipops
- Membre Naturel
- Messages: 18
- Enregistré le: 05 Nov 2007, 18:01
-
 par misslolipops » 11 Mai 2010, 22:43
par misslolipops » 11 Mai 2010, 22:43
Bonsoir je dois résoudre ce système et n'ayant pas suivant l'option maths l'an dernier, j'ai énormément de difficultés
Xn+1 = 5Xn
Yn+1 = 5Xn+5Yn
Zn+1 = -5Xn+3Yn+5Zn
Merci pour votre aide.

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 12 Mai 2010, 09:44
par Ericovitchi » 12 Mai 2010, 09:44
\ {=} \ \left[\begin{array}{CC} \begin{array}5 & 0 & 0\\ 5 &5 &0 \\ -5 & 3 & 5 \end{array} \end{array}\right] \ \left(\begin{array} X_{n}\\Y_{n}\\Z_{n} \end{array}\right))
donc matriciellement

et il faut que tu élèves la matrice à la puissance n. C'est une matrice triangulaire donc il y a des astuces autres que de la diagonaliser. Quoique. je te laisse chercher un peu.
Peut-être en l'écrivant 5I + Q et en appliquant la formule du binôme
-
misslolipops
- Membre Naturel
- Messages: 18
- Enregistré le: 05 Nov 2007, 18:01
-
 par misslolipops » 12 Mai 2010, 13:17
par misslolipops » 12 Mai 2010, 13:17
Je trouve par la méthode du pivot (la seule vue en cour) :
an= (5n+1) 5n
bn= 25.5n -1 (5n +1)
cn= 5n 5.5n + 5
Ensuite:
An = An.A^2 + bn.A + cn.I3

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 12 Mai 2010, 13:30
par Ben314 » 12 Mai 2010, 13:30
Je ne sais pas comment tu fait avec "la méthode du pivot" pour trover an, bn et cn, mais il y a des erreurs :
an, bn et cn sont tout les trois de la forme 5^n(polynôme en n)
et, au moins un des trois polynôme contient du n²...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
misslolipops
- Membre Naturel
- Messages: 18
- Enregistré le: 05 Nov 2007, 18:01
-
 par misslolipops » 13 Mai 2010, 18:50
par misslolipops » 13 Mai 2010, 18:50
il faut donc que je diagonalise A?
5-lambda 0 0
5 5-lambda 0
-5 3 5-lambda
-
ToToR_2000
- Membre Relatif
- Messages: 121
- Enregistré le: 26 Juin 2009, 17:33
-
 par ToToR_2000 » 13 Mai 2010, 19:10
par ToToR_2000 » 13 Mai 2010, 19:10
Pas besoin de diagonaliser, d'ailleurs rien ne dit qu'on peut a priori.
Il suffit de calculer
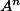
or A est triangulaire donc déjà tu connais la tête de la moitié supérieure + la diagonale. Reste 3 coefficients mais tu devrais pouvoir conjecturer leurs formes si tu calcules les premières puissances de A. Et tu termines par une récurrence.
-
misslolipops
- Membre Naturel
- Messages: 18
- Enregistré le: 05 Nov 2007, 18:01
-
 par misslolipops » 13 Mai 2010, 19:26
par misslolipops » 13 Mai 2010, 19:26
A^n = 5^n 0 0
5^n 5^n 0
-5^n 3^n 5^n
-
ToToR_2000
- Membre Relatif
- Messages: 121
- Enregistré le: 26 Juin 2009, 17:33
-
 par ToToR_2000 » 13 Mai 2010, 19:27
par ToToR_2000 » 13 Mai 2010, 19:27
Tu es sûr ?
-
misslolipops
- Membre Naturel
- Messages: 18
- Enregistré le: 05 Nov 2007, 18:01
-
 par misslolipops » 13 Mai 2010, 19:33
par misslolipops » 13 Mai 2010, 19:33
ah non du tout
-
ToToR_2000
- Membre Relatif
- Messages: 121
- Enregistré le: 26 Juin 2009, 17:33
-
 par ToToR_2000 » 13 Mai 2010, 20:21
par ToToR_2000 » 13 Mai 2010, 20:21
Et au hasard:
.n.5^{n-1}}{2} & 3n.5^{n-1} & 5^n\end{matrix}\right))
-
misslolipops
- Membre Naturel
- Messages: 18
- Enregistré le: 05 Nov 2007, 18:01
-
 par misslolipops » 13 Mai 2010, 21:32
par misslolipops » 13 Mai 2010, 21:32
comment trouver la tête de la matrice inférieure? puis une fois An connue que dois-je faire?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 13 Mai 2010, 22:39
par Ben314 » 13 Mai 2010, 22:39
Tout d'abbord, ta matrice, tu risque pas de la diagonaliser : rien qu'en la regardant, on voit que 5 est la seule valeur propre (triple) et qu'elle est pas diagonalisable...
La méthode "standard" pour ce genre de matrice, c'est celle que t'a donné Ericovitchi : tu écrit que
<br />=5I_3+N)
où
)
Tu calcule

et

puis tu utilise la formule du bonôme de Newton pour calculer
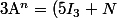^n)
(tu as le droit du fait que

et
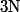
commutent)
Ca te donne en deux lignes le résultat de ToToR_2000.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
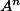 or A est triangulaire donc déjà tu connais la tête de la moitié supérieure + la diagonale. Reste 3 coefficients mais tu devrais pouvoir conjecturer leurs formes si tu calcules les premières puissances de A. Et tu termines par une récurrence.
or A est triangulaire donc déjà tu connais la tête de la moitié supérieure + la diagonale. Reste 3 coefficients mais tu devrais pouvoir conjecturer leurs formes si tu calcules les premières puissances de A. Et tu termines par une récurrence.<br />=5I_3+N) où
où )
 et
et  puis tu utilise la formule du bonôme de Newton pour calculer
puis tu utilise la formule du bonôme de Newton pour calculer 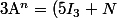^n) (tu as le droit du fait que
(tu as le droit du fait que  et
et 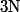 commutent)
commutent)