Salut,
Tout d'abord, pour faire un peu de "théorie", il faut un peu voir que, en dimension 3, quand on a une seule équation cartésienne, en général ça correspond à une surface (une sphére, un plan, un cône,...) et que si l'on veut seulement une courbe (une droite, un cercle, une élipse,...) il faut 2 équations, c'est à dire que l'on écrit la courbe comme intersection de deux surfaces.
Tu as surement déjà vu le cas des droites : pour définir une droite, il faut donner
deux équations de la forme ax+by+cz+d=0, c'est à dire que l'on est obligé de la définir comme intersection de deux plans (et il y a évidement des tas de choix possibles pour les deux plans...).
Tout ça pour dire que, ton intersection de deux sphéres qui est un cercle, il n'y a aucun espoir de le définir avec
une seule équation mais il en faudra forcément deux.
On peut évidement... ne rien faire du tout et garder les deux équations des sphères de départ mais on peut aussi essayer de donner deux équations les plus simples possibles.
A mon avis, deux équations trés naturelles, ça serait :
-Une équation du plan qui contient le cercle.
-Une équation de la sphére
centrée en un point du plan qui contient le cercle (comme ça le rayon du cercle serait le même que celui de cette sphère)
Tu as déjà trouvé une équation du plan P contenant le cercle : x+3y=6
Pour trouver une équation de la sphère centrée en un point de P qui contient le cercle, tu as (au moins) deux méthodes :
1) Méthode "Géométrique" : Tu trouve le centre de cette sphère en cherchant l'intersection du plan P et de la droite (O1O2).
C'est ce que tu as commencé à faire, sauf que la droite (O1O2) ce n'est surement pas "x+3y", vu que
-Au minimum il faudrait un "=quelque chose" pour que ça fasse une équation !!!
- Avec
une seule équation ax+by+cz+d=0 , ça ne fait jamais une droite mais un plan donc il te faut une deuxième équation.
Par exemple,
des équations de la droite (O1O2) ça serait 3x-y=0 et z=0 (qui sont bien vérifiées par O1 et par O2).
Plus simplement, tu peut aussi dire q'un point M est sur la droite (O1O2) ssi il existe un réel t tel que
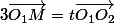
ce qui signifie que M a des coordonnées de la forme (t,3t,0) où t est un réel [ça s'appelle une équation paramétrique]
Une fois le centre trouvé, tu peut faire un petit dessin en dimension 2 qui se place dans un plan contenant les points O1 et O2 où les deux sphères apparaissent comme des cercles et le cercle que l'on cherche apparait comme 2 points. Cela te permet de voir comment se calcule le rayon r du cercle en fonction des rayons R1 et R2 des deux sphères et de la distance O1O2 entre les deux centres.
2) Méthode analytique : tu as déja montré que l'intersection des deux sphères est l'ensemble des points (x,y,z) tels que :

(intersection d'un plan et d'une sphère)
Sauf qu'il y a des tas de sphères différentes dont l'intersection avec le plan x+3y=6 donne ce même cercle (essaye de le visualiser...) et, pour obtenir ces différentes sphères, on peut avoir l'idée de dire que, pour tout réel k, le système ci dessus est équivalent à :
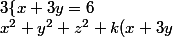=6+6k\right.)
La deuxième équation est celle d'une sphére (qui dépend de k). Il ne reste plus qu'à regarder où est son centre et à déterminer k de façon à ce que le centre soit dans le plan x+3y=6.
Remarque : Tu peut aussi regarder, en fonction de k, quel est le rayon de cette sphère puis à chercher pour quel k ce rayon est minimal. Tu obtient comme par hasard la même chose (comprend tu pourquoi ?)
Bon, je me rend compte que j'en ait écrit des tartines...
Le principal c'est quand même l'idée que :
Cercle = courbe (et pas surface) = deux équations cartésiennes.
