Bonjour
comment montrer que
fn(x) = (1 + x/n)^n.converge uniformement sur
[-a,a] quelque soit a positif
avec |ln(1+x)-x|<=Cx² pour x appartenant à [-1/2,1/2]
C>0
j'ai deja etudier la convergence simple et fn converge simplement vers la fonction exp(x)
Convergence Uniforme Suite De Fonction
3 messages
- Page 1 sur 1
par Ericovitchi » 10 Mai 2010, 10:10
La suite de fonction (1+x/n)^n converge simplement vers e^x.
Pour montrer qu'elle converge uniformément vers f il faut montrer que
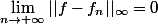
(en notant f -->|)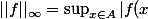
)
il faut donc majorer^n|)
et c'est là qu'il te servir de ce que tu as démontré avant
^n|=|e^x-e^{n.ln(1+x/n)}|=e^x|1-e^{n.ln(1+x/n)-x}|=e^x|1-e^{n(ln(1+x/n)-x/n)}|)
hors tu avais démontré qu'il existait C tel que |ln(1+x/n)-x/n|<Cx²/n² donc
^n|<e^x|e^{Cx^2/n}-1|)
qui tends bien vers zéro
Pour montrer qu'elle converge uniformément vers f il faut montrer que
(en notant f -->
il faut donc majorer
et c'est là qu'il te servir de ce que tu as démontré avant
hors tu avais démontré qu'il existait C tel que |ln(1+x/n)-x/n|<Cx²/n² donc
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :