Exercice : Intégrale

[Zaaroth]

Bonjour !

Je suis coincé sur un exo ou je n'arrive pas une ou deux question ( même si il me semble que les réponses sont toutes bêtes ).

Voici l'énoncé :

Soit n , un entier naturel non nul. On appelle fn la fonction définie sur [0,+infini[ par fn(x)= ln(1+x^n) et on pose In= integrale1-0 ( je ne sais pas comme symboliser sur le site :triste: ) ln(1+x^n) dx.

On note Cn la courbe représentative de fn dans un repère orthonormal ( O,i,j ).

1)a- Déterminer la limite f1 en +infini
b- Étudier les variations def1 sur [0,+infini[
c- A l'aide d'une intégration par parties , calculer I1 et interpréter graphiquement le résultat.( Pour le calcul de I1, on pourra utiliser le résultat suivant : pour tout x appartenant a [0,1], x/(x+1)= 1-1/(x+1) )

J'ai fait cette partie


2)a- Montrer que pour tout entier non nul n , on a 0 <(ou égal) In <( ou égal) ln(2)

b- Etudier les variations de la suite In
c- En déduire que la suite In est convergente

Je bloque totalement a cette partie par contre ...

3)Soit g la fonction définie sur [0,+inifini[ par g'x)=ln(1+x)-x
a- Etudier le sens de variation de g sur [0,+infini[ et en déduire le signe de g sur cet intervalle. ( Fait)

b-Montrer alors que pour tout entier naturel n non nul , et pour tout x réel positif , on a :
ln(1+x^n) <( ou égal ) x^n

c- En déduire la limite de la suite In

Je bloque pour ces deux la aussi

Merci d'avance pour l'aide !

[Arnaud-29-31]

Bonsoir,

Pour montrer que , il faut essayer d'encadrer In sachant que comme , alors et le log étant une fonction croissante, .

Pour les variations, on étudiera simplement le signe de

La c) se déduit facilement de la a) et la b).

[Zaaroth]

Merci je vais essayer ca !

Par contre pour ca : "on étudiera simplement le signe de I_{n+1} - I_n" , je comprend pas trop :hein: ainsi que la 3)b- !

[Arnaud-29-31]

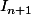Et bé oui, tu regardes ce que donne pour savoir si est supérieur ou bien inférieur à I_n, pour déduire la croissante ou la décroissance.

Pour la 3b, on étudiera la fonction et on montrera qu'elle est toujours négative ou nulle ... On pourra commencer par la dériver et il apparaît quelque chose de pas mal ...

[Zaaroth]

C'est bon j'ai tout réussi :id: merci beaucoup