Bonjour tout le monde,
Voilà mon fils qui est en 4ème à un devoir maison de maths à finir pour demain et franchement mon mari et moi en perdons notre latin...
Pourriez-vous nous donner une petite piste ? :hein:
voici l'énoncé :
Narration de recherche
On construit des figures avec des carrés, on associe à chaque figure le nombre de carrés qui la constituent
a1 = 1 carré
a² = 5 carrés : on ajoute des carrés autour de la figure précédente
a3 = 13 : on ajoute des carrés autour de la figure précédente
On continue ainsi ces constructions. Déterminer a4, a5, ....., a10, .....
Donner la formule générale pour aN (a exposant n -je ne sais pas comment le faire au clavier-)
Pour les dessins qui illustrent l'exercice en fait à chaque tour on ajoute des carrés tout autour de la figure par couche successive (j'espère que ce n'est pas trop confus sans dessin)
En tout cas merci d'avance à toutes les personnes qui pourront nous aider.
2 parents nuls en maths :happy2:
Figures avec des carrés
7 messages
- Page 1 sur 1
Voila, si j'ai bien comprit le principe, on a cette figure :

On voit que sur la diagonale que je trace on a un carré de plus à chaque ajout.
Il y a 4 diagonales donc à chaque fois que l'on rajoute des carrés, on en ajoute 4 de plus que la fois d'avant.
Pour passer de à
à 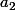 , on ajoute 4 carrés
, on ajoute 4 carrés
Pour passer de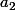 à
à 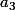 , on ajoute 8 carrés
, on ajoute 8 carrés
Pour passer de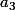 à
à 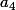 , on ajoute 12 carrés
, on ajoute 12 carrés
etc ...
Pour passer de à
à  , on ajoute 4.n carrés
, on ajoute 4.n carrés
(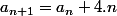 ).
).
Finalement,\right))
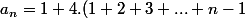 = 1 + 4.\frac{n.(n-1)}{2} = 1 + 2.n(n-1))

On voit que sur la diagonale que je trace on a un carré de plus à chaque ajout.
Il y a 4 diagonales donc à chaque fois que l'on rajoute des carrés, on en ajoute 4 de plus que la fois d'avant.
Pour passer de
Pour passer de
Pour passer de
etc ...
Pour passer de
(
Finalement,
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
