Limite de suite

par **extasy** » 04 Mai 2010, 16:13

Bonjour, j'aimerai savoir quelle est la limite de

quand n tend vers l'infini.

Merci

par **Micki28** » 04 Mai 2010, 16:19

Bonjour,

Il faut faire un encadrement puis appliquer le théorème des gendarmes.

Tu sais que:

-1 =< cos n =< 1

A toi de jouer !

par **extasy** » 04 Mai 2010, 17:05

D'accord, quel est l'encadrement de

?

par **Micki28** » 04 Mai 2010, 17:07

Un = cos(n)/n

Donc tu pars de:

-1 =< cos (n) =< 1

Pour retrouver Un, il faut que tu fasses quoi d'après toi?

Tu as cos (n) et il faut avoir cos (n)/n comment tu passes de l'un à l'autre?

par **extasy** » 04 Mai 2010, 17:09

On divise par n pour passer de l'un à l'autre ...

par **Micki28** » 04 Mai 2010, 17:16

Oui ! Cependant n ne doit pas être égal à 0 ! Mais ça on s'enfou car n tend vers l'infini !!!

Tu as dons:

-1/n =< cos(n)/n =< 1/n

Maintenant... Théorème des gendarmes !!!

Et tu trouves que lim Un = 0

par **extasy** » 04 Mai 2010, 17:22

Le théorème des gendarmes dit : Si les suites v et w convergent vers L et si, à partir d'un certain rang, w_{n}\leq{u_{n}}\leq{v_{n}} alors la suite u converge elle aussi vers L.

par **extasy** » 04 Mai 2010, 17:23

Pardon petit problème ^^

Le théorème des gendarmes dit : Si les suites v et w convergent vers L et si, à partir d'un certain rang,

alors la suite u converge elle aussi vers L.

par **Dinozzo13** » 04 Mai 2010, 17:24

Salut !
Pour tout

:

Pour tout

:

Or

donc d'après le théorème des gendarmes

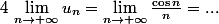
Edit : grillé :ptdr:

par **Dinozzo13** » 04 Mai 2010, 17:27

extasy a écrit:Pardon petit problème ^^

Le théorème des gendarmes dit : Si les suites v et w convergent vers L et si, à partir d'un certain rang, alors la suite u converge elle aussi vers L.

En effet :+++:

par **extasy** » 04 Mai 2010, 17:37

Limite de 1/n = 0 donc limite de un=0.

par **Dinozzo13** » 04 Mai 2010, 17:39

En effet
:+++:

par **extasy** » 04 Mai 2010, 17:41

D'accord, bon ben merci à tous pour votre aide !!!

par **Dinozzo13** » 04 Mai 2010, 17:55

De rien :++:
revient quand tu veux

par **extasy** » 04 Mai 2010, 18:12

Merci, c'est génial :+:

Limite de suite

Limite de suite

Qui est en ligne