Résolution d'équation de trigonométrie 1ereS

[fafaky]

Bonjour :)
Je dois résoudre quelques équations de trigonométrie incluant la tangente:
tan(x)=;)3 , tan(x)=(;)3)/3 et tan(2x)=1

J'ai la méthode qui consiste à aboutir avec des égalités telles que cosx= cosa ou sin x = sin a ... mais je n'arrive pas a finir.

Voila ce que j'ai pour l'instant :
tan(x)=;)3
sin(x)/cos(x) = ;)3
sin(x)=;)3*cos(x)
cos(;)/2 - x)=;)3*cos x

Merci pour votre aide :)

[Dinozzo13]

Salut !
Attention : la fonction tangente est définie sur

[Dinozzo13]

De plus, je pense que ce que tu a fait ne t'amène à rien.
Je tenterai plus cela :

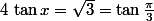
[fafaky]

Okay merci :) Mais a partir de tan(x)=;)/3 je suis bloquée :/ Je ne connais aucunes formules de résolution d'équation avec la tangente donc je serais obligée de me ramener à ce que j'ai fait précédemment avec
tan(x)=sin(x)/cos(x) :hum:

[Dinozzo13]

En effet, après tu feras un produit en crois et tu changeras tout de manière à avoir uniquement du cosinus ou du sinus :++:

[Dinozzo13]

Mais a partir de tan(x)=;)/3

Attention : :+++: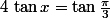

[fafaky]

Okay je suis blindée pour faire toutes mes équations la :D merci beaucoup.
Hum derniere petite chose, je comprend pas pourquoi tu dis que
tan x= ;)3 = ;)/3 :hein:

[Dinozzo13]

Erreur, j'ai dit :

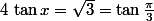
bah comme ça, ça permet de faire intervenir la tangente pour pouvoir ensuite tout transformer en sinus ou cosinus sinon, on sait pas résoudre sans.

[Dinozzo13]

Pour info, je trouve vite fait pour solution de l'équation , tout les réels de la forme .
Reste à confirmer ces solutions :++: