Carré parfait
17 messages
- Page 1 sur 1
On considère l'ensemble suivant :
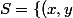\in\mathbb{N}^{2}\setminus\exists k\in\mathbb{N}^{2}\,:\,\frac{x^{2}+y^{2}-x}{xy}=k\right\})
Montrons que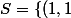\right\}) .
.
Parmi tous les couples de , considérons le couple
, considérons le couple ) qui minimise la somme
qui minimise la somme 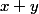 . Sans perte de généralité, on peut toujours supposer
. Sans perte de généralité, on peut toujours supposer 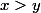 (*). Considérons l'équation du second degré suivante (obtenue en "cassant" la fraction de S) :
(*). Considérons l'équation du second degré suivante (obtenue en "cassant" la fraction de S) :
 + y^2 = 0)
On sait que vérifie cette dernière. On cherche à exprimer la deuxième racine
vérifie cette dernière. On cherche à exprimer la deuxième racine  . D'après les relations de Viète, on a :
. D'après les relations de Viète, on a :

En particulier, est un entier. De plus, d'après notre équation, on a :
est un entier. De plus, d'après notre équation, on a :

Ainsi\in S) . Mais
. Mais  , d'où
, d'où  , ce qui contredit la minimalité de
, ce qui contredit la minimalité de 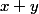 . Ainsi
. Ainsi  .
.
 , d'où
, d'où 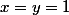 . En particulier
. En particulier  (et
(et  ) est bien un carré parfait.
) est bien un carré parfait.
(*) On peut car le fait d'échanger et
et  n'affecte pas le signe du numérateur. De plus, si on considère
n'affecte pas le signe du numérateur. De plus, si on considère 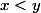 , alors on choisit
, alors on choisit ) de sorte que
de sorte que 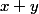 soit maximale.
soit maximale.
Montrons que
Parmi tous les couples de
On sait que
En particulier,
Ainsi
(*) On peut car le fait d'échanger
Aprés quelque calculs, je trouve qu'effectivement on doit avoir x=d² et, parmi les différentes solutions (il y en a d'autres) si d distinct de 1 :
y=d ou bien y=d(d-1) ou bien y=d(d+1) ou bien y=d(d-1)(d+1)
P.S. : la méthode de résolution est assez "standard", on pose d=pgcd(x,y) puis on regarde...
y=d ou bien y=d(d-1) ou bien y=d(d+1) ou bien y=d(d-1)(d+1)
P.S. : la méthode de résolution est assez "standard", on pose d=pgcd(x,y) puis on regarde...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
ça me semble bien compliqué dans un tel cas :
Si d=pgcd(x,y) alors x=dx' , y=dy' où pgcd(x',y')=1.
L'équation devient dx'y' | dx'²+dy'²-x' qui implique que d|x' mais aussi que x'|dy'² c'est à dire (Lemme de Gauss) que x'|d.
On a donc x'=d et x=dx'=d².
Si d=pgcd(x,y) alors x=dx' , y=dy' où pgcd(x',y')=1.
L'équation devient dx'y' | dx'²+dy'²-x' qui implique que d|x' mais aussi que x'|dy'² c'est à dire (Lemme de Gauss) que x'|d.
On a donc x'=d et x=dx'=d².
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
17 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 19 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
