Matrice

[polka-dots]

bonsoir, j'ai beaucoup de mal avec les matrices alors j'aurais plusieurs questions:

On me demande si était surjective et injective, B étant une matrice.

On me propose comme correction:

B est inversible. Soit Y une matrice de M2(R) et X= Y, alors = Y, donc est surjective.
J'arrive pas à comprendre pourquoi on a utilisé l'inverse pour montrer la surjectivité, et en quoi = Y montre que c'est surjectif.

Pour la bijectivité, on me dit: " Comme M2(R) est un espace vectoriel de dimension fini 4, alors c'est forcément bijectif". Là je n'ai pas compris non plus.

Merci pour votre aide!

[gigamesh]

bonsoir,
la définition de la surjectivité c'est que tout élément de l'ensemble d'arrivée a (au moins) un antécédent.

Dans la démarche que tu nous exposes, on choisit un Y (n'importe lequel !) en on montre que est un antécédent de Y.

Donc tout Y admet ...

[polka-dots]

oui mais ça ne nous dit pas qu'il y en a plusieurs, on pourrait juste conclure que c'est bijectif non?

[polka-dots]

Oui non c'est bon en faîte. Et pour la bijectivité?

[gigamesh]

Pour prouver que tu as une surjection, tu n'as pas besoin de prouver l'unicité de l'antécédent.
Qu'il y ait un ou plusieurs antécédents ne nous intéresse pas, dans un premier temps.

Attention, bijectif signifie injectif et surjectif.

Ton "juste conclure que c'est bijectif" me semble bizarre... La bijectivité est une propriété plus forte que la surjectivité. A moins que ton "juste" signifie "directement" ?

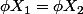
Pour conclure à l'injectivité, tu peux dire que implique par linéarité.

Evidemment,on a envie de conclure qu'on a alors, car cela prouve l'injectivité et donc la bijectivité.

Il faut juste soigner l'argumentation, car quand on travaille avec des matrices un produit peut être nul sans qu'on ait un facteur nul.

Ou bien tu utilises le fait qu'en dimension finie, si f est un morphisme d'un ev dans lui-même, alors f bij f inj f surj. Une démonstration de cours à connaître...

[polka-dots]

Oui, je voulais directement. Ok, ça y est c'est compris, en tout cas merci beaucoup!