Inversibilité modulo n (crypto/arythmétique)

[Tinoute]

Bonjour !!
J'ai deux questions sur l'inversibilité d'entiers dans les congruences :

1°) "Calculer le nombre d'éléments inversibles dans Z/415800 Z" (Z étant l'ensemble des nombres entiers relatifs, je ne sais pas faire la double barre pr les ensembles ...)

j'ai bien fait la décomposition en facteurs premiers :
415800=2^3*3^3*5^2*7*11
donc pour que k soit inversible, il faut qu'il ne soit multiple d'aucun des nombres {2,3,5,7,11} car il doit être premier avec 415800.

Mais là, je sèche ... (j'imagine qu'il y a plus simple que de calculer tous les premiers et leurs combinaisons possibles :hum: ...)

2°) Quels sont les éléments inversibles de Z/13Z ? Pout a=6, et i entier, calculer a^i [13]. Que constatez vous ? Quels sont les éléments qui sont des carrés modulo 13 ?"

bon les éléments inversibles, vu que 13 est premier sont les entiers de 1 à 12.
Ensuite, les puissances de 6 :
6^0=1[13]
6^1=6[13]
6^2=10[13]
6^3=8[13]
6^4=9[13]
6^5=2[13]
6^6=12[13]
6^7=7[13]
6^8=3[13]
6^9=5[13]
6^10=4[13]
6^11=11[13]
6^12=6[13]
6^13=10[13]
ensuite on retrouve 10 puis 8 puis 9, ...

Bon, ben je remarque que tous les nombres inversibles apparaissent comme puissance de 6 modulo 13.
Mais quels sont les carrés modulo 13 ???
toutes les puissances paires de 6 le sont (donc 10,9,12,3,4,6) mais est ce que c'est les seuls ?? Sinon, les quels autres ???


Merci au moins d'avoir lu le meessage, et merci encore plus si vous pouvez éclairer ma lanterne !!

[benekire2]

Tu recherche en fait c'est le nombre de nombres inférieurs à 415800 qui lui sont premiers. Il y a une "formule" , c'est l'indicatrice d'Euler :



avec ici n=415800

bien sur les p_i c'est la décomposition et les k les coefficients.

C'est relativement facile à retrouver, de manière intuitive.

[Ben314]

Salut,
Pour ta première question, le nombre d'élément inversible de Z/nZ est noté on peut montrer que, si la décomposition de n en facteurs premiers est 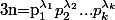alors .
La preuve de ce résultat est assez simple : on commence par regarder le cas où où les éléments inversibles sont ceux non divisible par puis on utilise le théorème dit "chinois" qui affirme que, si a et b sont premiers entre eux, alors Z/abZ est isomorphe à (Z/aZ)x(Z/bZ) pour le cas général.

Pour ta deuxième question, tu t'est forçément trompé dans les calculs, vu que tu trouve 6^12=6^1 mais 6^11 différent de 6^0 (comme 6 est inversible modulo 13, on peut "diviser" par 6)
Si tu ne te trompe pas, tu devrait trouver 6^12=1 (Le petit théorème de Fermat dit que, si p est premier et n non divisible par p alors n^(p-1)=1 modulo p)
Enfin, pour savoir qui sont les carrés (non nuls) de Z/13Z, tu as raison, tout les 6^pairs sont évidement des carrés et ils représentent la moitié des éléments non nuls.
Il ne peut pas y avoir d'autres carrés car si on regarde le carré de tout les éléments de Z/13Z, comme y²=x² y=x ou y=-x, le nombre de carrés non nuls est exactement la moitié du nombre d'éléments non nuls.

[Tinoute]

Merci !! =}