Produit fini ,analyse complexe

[stellabellaparis01]

SLT
merci de m'avoir aider pour calculer ce produit

produit fini de k=1 à k=n+1: [1+exp^[i*t/(2)puissance k]]

[Ben314]

Peut-être qu'en mettant sous forme polaire...
[il est bien connu que les produits sont plus façile à calculer sous forme polaire]

On pourra bien entendu s'aider d'un dessin pour trouver le module et un argument de avec 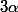réel...


Edit : on obtient une expression assez simple d'un argument du produit, mais pour le module, c'est pas trés simple...

[stellabellaparis01]

merci mais comment polaire est ce que tu peux m'expliquer s'il tu plaît

[Ben314]

Fait un dessin : on voit assez clairement quoi prendre comme argument.
Ensuite, tu met exp(i*argument) en facteur et tu trouvera une expression plus agréable de 1+exp(i.alpha).

[stellabellaparis01]

merci
je vais essayé de trouver la solution

[stellabellaparis01]

dsl mais jz n'ai pas trouvé la solution :mur: :mur:

s'il vous plait aidez moi

[Ben314]

[stellabellaparis01]

salut
merci de m'avoir aider mais j'ai pas trouver la solution
est ce que tu me montrer toute les étapes pour calculer

de k=1 à l'infini
;)[ (1+;)it/ 2^k )/2] = ;)[ 1+ (1/2)* [ -1+;)xp( it/ 2^k ) ] ]

je dois la trouvé de cette forme
[-1+exp (i*t) ] * 1/2

je vous remerci

[Ben314]

Effectivement, il y a une "astuce" :
Pose puis calcule pour n=1, puis n=2, puis n=3...
Que constate tu ?
Démontre le (par récurrence).
Cela te permet d'avoir une forme bien plus simple pour et en particulier de trouver la valeur de ton produit infini.