Devoir sur les suites

[blopishere]

Bonjour!
Nous avons abordé les suites en cours, un sujet qui ne m'est vraiment pas aisé...

Notre devoir porte sur les limites des suites réelles :

Pour tout n appartenant à N*, on pose :
u(n) = (n/(n^2 +1))+(n/(n^2 +2))+...+(n/(n^2 +n))

J'ai réussi la première question (•de combien de termes u(n) est-il la somme? n termes puisque la suite commence par 1
•Quelle est la limite de chacun de ces termes quand n tend vers + l'infini? Peut-on en déduire la limite de u(n) quand n tend vers + l'infini ? toutes les limites sont égales à 0, on peut trouver la limite de u(n) par théorème d'opération, et c'est donc aussi égal à 0...)

J'espère que pour l'instant je ne suis pas dans l'erreur!

La deuxième question me pose problème :
Quel est le plus petit de ces termes? Quel est le plus grand?
(Je ne vois pas trop comment faire, vu que n peut être aussi grand que l'on veut, ou peut valloir 1... Y a-t-il plusieurs cas?)
En déduire que pour n>= 1,
(n^2 /((n^2 +n)) <= u(n) <= (n^2 /(n^2 +1))

Mais comment peut on faire?
Pourriez vous me donner une piste?
Merci beaucoup!

[Mikou]

il suffit detudier la fonction x/(x²+x)

[El_Gato]

Salut

Pour tout n appartenant à N*, on pose :
u(n) = (n/(n^2 +1))+(n/(n^2 +2))+...+(n/(n^2 +n))

J'ai réussi la première question (•de combien de termes u(n) est-il la somme? n termes puisque la suite commence par 1
•Quelle est la limite de chacun de ces termes quand n tend vers + l'infini? Peut-on en déduire la limite de u(n) quand n tend vers + l'infini ? toutes les limites sont égales à 0, on peut trouver la limite de u(n) par théorème d'opération, et c'est donc aussi égal à 0...)

J'espère que pour l'instant je ne suis pas dans l'erreur!

Hélas si. Chaque terme tend vers 0 mais tu ne peux pas en déduire que la suite u(n) tend vers 0 car, quand n augmente indéfiniment, le nombre de ces termes croît lui aussi indéfinimment. On est donc en présence d'un type "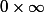 et on ne peut pas conclure. D'où la deuxième partie de ton exo:

La deuxième question me pose problème :
Quel est le plus petit de ces termes? Quel est le plus grand?
(Je ne vois pas trop comment faire, vu que n peut être aussi grand que l'on veut, ou peut valloir 1... Y a-t-il plusieurs cas?)
En déduire que pour n>= 1,
(n^2 /((n^2 +n)) <= u(n) <= (n^2 /(n^2 +1))

Le plus petit des termes dans u(n) (il n'y en a que n) est évidemment le premier, le plus grand le dernier. Comme tous ces termes sont positifs, u(n) est plus grand que n fois le plus le plus petit, et plus petit que n fois le plus grand, d'où les inégalités demandées.
De la dernière inégalité, tu vois que u(n) tend vers 1 quand n augmente indéfinimment, et non pas 0 comme tu l'avais crû au début.

[blopishere]

Merci de me montrer mon erreur!

Comment peut-on trouver l'inégalité de la question avec seulement ces informations?

[tigri]

bonsoir
le pus petit, ou le plus grand des termes : cela concerne les termes de la somme qui constitue Un
chaque terme est une fraction : même numérateur ; donc la pus petite est celle qui a le pus grand dénominateur ..........
il y a n fractions dans la somme Un.......