Espace vectoriel.

[juliette92]

Bonjour,

Soient ( E ,+,. ) un espace vectoriel de dimension finie n , u et v deux
endomorphismes de E tels que :
u°v=0 et u+v est inversible .

(a) Montrer que : Im(u) + Im(v) = E .
(b) Montrer que : rg(u) + rg(v) = dim(E) .

Je pense que je peux me servir du fait que Im(u+v) est inclus dans Im(u)+Im(v) mais j'ai besoin de plus de précisions..

merci d'avance.

[Nightmare]

Salut !

C'est une bonne idée, il suffirait donc de montrer que Im(u+v)=E, mais on te dit que u+v est inversible ...

[juliette92]

ça parait simple mais je ne vois pas le truc évident lié au fait que u+v est inversible... :s

[Nightmare]

que veut dire être "inversible" pour toi ?

[juliette92]

Inversibles : appartient à GL(E) donc endomorphisme bijectif,
donc injectif, donc le noyau est le vecteur nul , donc sa dimension est nulle..
Théoreme du rang : dim(E) = dim (Ker(u+v)) + dim(Im(u+v))
soit dim(E) = dim(Im(u+v)) ???

[Nightmare]

La première phrase suffit ! u+v est bijectif donc son image (ie l'ensemble des valeurs qu'elle prend) est bien E tout entier non?

[juliette92]

OUi oui je suis d'accord ! Donc j'ai une inclusion, reste à prouver l'égalité des dimensions...

[Elendil974]

Bonsoir,


Montrons que E=Im(u)+Im(v)

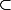est évidente



Soit x E

on note w=(u+v)^(-1) car u+v inversible

on a x=(u+v)ow(x)=u(w(x))+v(w(x))

donc x Im(u)+Im(v)

d'où l'inclusion.

Pour la seconde question on utilise la formule de grassmann et il reste donc juste à montrer que dim(Im(u) Im(v))=0

Soit xIm(u) Im(v)

donc il existe yE tel que:

v(y)=x

on compose par u d'où u(v(y))=u(x)=x car xIm(u)

or uov=0 donc x=0 d'où l'égalité!