Exercice de mathématique.

[lemarchand]

Bonjour,

un exercice de math me pose problème, je comprend les première question, mais les autres reste un mystère pour moi.

http://up.sur-la-toile.com/izCQ (Je tient à préciser que j'ai recopier l'énoncer moi-même afin de respecter la charte du forum.)

1°) Pour la première question pas de difficulté je me suis aider de la propriété des angles dans un triangle et j'ai trouver 180/7 donc en radian : Pi/7.

2°) Pour la seconde j'ai des pistes, il faut que je trouve 2 angles donc si je comprend puisque les angles ADB et ABD sont égaux étant donné qu'on se trouve dans un triangle isocèle. Je pense qu'il faut se servir d'une propriété que j'ai oublie pour dire que BAC et BDC sont égaux ? ensuite pour l'angle BAD je voulais avoir confirmation qu'il faillais dire que BAD = 180 - 5a = Pi-5a ?

3°) faut-il se servir de cette relation b²=a²+c²-2ac.cosB
c² = ...
a² = ...
J'ai essayer cette méthode, mais il faut exprimer pas mal de chose en fonction de x.

4°) à 6°) ...pas encore d'idée de recherche...

7°) Je ne voit pas sous quelle forme sera le résultat, je remplace x par cos(Pi/7). Fonction trinôme ?

Merci !

[Ben314]

Salut,
Bon, j'arrive pas à ouvrir ton fichier (pas d'extention...) donc, sans énoncé, je suis un peu sec...

essaye de rectifier le tir (ajout d'une extention ? , nouveau fichier ?...)

[lemarchand]

petit fichier: Exercice.txt

Grâce au bloc note.

[Ericovitchi]

Il s'ouvre avec Word.

Oui BAD = 180 - 5a et puis tu peux dire aussi que la somme des angles de BAD est égale à 180 donc que 2 ABD + 180 - 5a= 180

non pour le 3 fais plus simple. En projetant A sur BC tu vois déjà que
cos a = (x/2)/ AB mais tu sais aussi que CD=BC=x et dans ce triangle BCD tu peux écrire des expressions aussi (cos a/2= ? )

[lemarchand]

Bonjour, voilà où j'en suis :

1°) a = Pi/7 rad
2°)Je n'est pu déterminer que l'angle DAB = Pi-5a
3°) Je trace la hauteur de sommet A "de base" H, donc étend donné que ABC est isocèle, BH = x/2.
Donc arrivé ici je peux utilisé la formule du cosinus = coté adj/hypothénuse =(x/2)/cos a et là je suis bloqué car je doit l'exprimer en fonction de x seulement...
4°) Bloqué...
5°) sin (a+b)= sina.cosb + sinb.cosa en partant de : sin 3x = sin(2x+x) =sin2xcosx + sinxcos2x" bloqué à ce stade là.
6°)Bloqué...
7°) Compris
8°) Voilà ce que je trouve avec la calculette graphique : http://img121.imageshack.us/img121/4736/sany1349.jpg

[Ben314]

1) a=pi/7 : OK (car la somme des angles de ABC vaut pi)

2) DAB=pi-5a : OK, mais on peut simplifier vu que pi=7a.
Pour les autres angles, c'est nettement plus astucieux. Une méthode :
Si on note b l'angle ABD, la somme des angles du triangle ADB vaut pi donc l'angle ADB=pi-...=... (ne pas oublier que pi=7a).
Sauf que CBD=...+...=... est égal à ADB vu que le triangle CBD est isocéle en C donc ...=... ce qui donne b=...

Je ne pense pas que tu puisse faire grand chose dans la suite de l'exercice sans avoir les angles du triangle ADB.

En particulier, pour le 3), on te demande les longueurs uniquement en fonction de x et pas en fonction du cos ou du sin de a.
Si tu ne te trompe pas pour le 2), tu as du obtenir que ADB est isocèle en D et cela permet de trouver trés simplement AD puis d'en déduire AC puis AB (comme ça, tu as toutes les longueurs de la figure uniquement en fonction de x)

4) De nouveau, il faut absolument avoir fini le 2) et le 3) ensuite... loie des sinus dans des triangles bien choisis...

5) Il y a une faute de frappe dans ton fichier .txt : il faut montrer que
sin(3a) = sin(a)[4cos²(a)-1]
Ce qui se fait uniquement à l'aide des formules trigo (donc rien à voir avec ce qui précède)

6) Déduction immédiate du 4) en utilisant la formule du 5)

7) Déduction simple du 6)

8) On voit rien sur ta photo, mais, le but est effectivement de trouver une approximation d'un x tel que .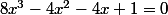
Si ta machine trace des courbe, tu peut l'utiliser ici : tu demande des "zooms" de plus en plus gros pour avoir un peu de précision.

[lemarchand]

Voilà où j'en suis, j'ai avancé :

1°) OK
2°) j'ai trouve ceux-ci : l'angle ADB = (180-a)/2 ou (Pi-a)/2
l'angle ABD = (180-2a)/2 ou (Pi-2a)/2
l'angle DAB = 180 - [(180-a)/2 + (180-2a)/2] = (2Pi-3a)/2 bloqué à ce stade.

3°)Je sais que les angles DBA et DAB sont égaux, donc le triangle ABD est isocèle.
Donc AC = x-1
AB = x-1 car ABC est isocèle en A donc AC = AB.

4°) j'utilise une des formule du cours :
(x)/(sin angleD) = (x)/(sin angleB) = (1)/(sin angleC)

<==> on trouve à la fin donc, après un produit en croix : x = (sin3a)/(sina)
est-ce bon ?

Pour le second on utilise la même formule :
(x-1)/(sin angleD) = (1)/(sin angleB)
<==> (x-1)/(sin3a) = (1)/(sin2a)
<==> x-1 = (sin 3a)/(sin 2a)

est-ce bon ?

5°) sin 3a = sin(2a + a)
= cos 2a. sin a + sin 2a.cos a
= sin a.(2cos²a-1) + (2cos a.sin a)cos a
= sin a.(2cos²a-1) + (2cos²a.sin a)
= sin a.(4cos²a-1)

Est-ce bon ?

6°) x = (sin 3a)/(sin a)

d'où x = (sin a.(4cos²a-1))/sina
x = 4cos²a-1

x-1 = (sin 3a)/(sin 2a)


d'où x = 1 = (sin a.(4cos²a-1))/2cos a
<==> (sin a.(4cos²a-1))/(2cos a.sin a) On simplifie par sin a
<==> x-1 = (4cos²a-1)/(2cos a)

est-ce bon ?

7°) bloqué
8°) S j'a ben compris, à l'aide de ma calculette graphique je doit tracer la courbe donc comme sur mon image, et en faisant un zoom sur le point d'intersection de la courbe avec l'axe des abcisse ?

Merci de ton aide !

[Ericovitchi]

C'est celle qui est près de 1. Elle vaut ~0.900969

[lemarchand]

C'est celle qui est près de 1. Elle vaut ~0.900969

Merci, mais une petite question pourquoi l'autre point d'intersection sur l'intervalle [0;+OO[ n'est pas solution ?

[Ericovitchi]

tu as démontré que cos(pi/7) était solution de 8x^3 -4x²-4x+1 = 0
mais rien n'empêche cette équation d'en avoir 2 autres.

Alors pourquoi c'est celle-là et pas une autre ? c'est juste une question de plage de valeurs l'angle pi/7 est assez petit donc le cos est assez proche de 1.
L'autre valeur vaut ~0.222521