Codage décodage

[chtirico]

Bonjour,

pourriez vous me donner des indications pour mon exercice. J'ai réussi les3 premières questions mais après je bloque.

On considère les 10 caractères A B C D E F G H I J auxquels on associe dans l ordre les nombres entiers de 1 à 10. on pose V={1,2,3,4,5,6,7,8,9,10}

1a) démonstration de cours : demontrer que si a congru b [11] et c congru d[11] alors ac congru bd [11].

1b) en deduire que si a congru b [11] alors a^n congru b^n [11].

2) on désigne par f lafonction définie sur V par f(n) est le reste de la division euclidienne de 5^n par 11. Coder BACF. Peut on décoder le message sans ambiguité.

3) on désigne par g lafonction définie sur V par f(n) est le reste de la division euclidienne de 2^n par 11. Etablir la grille de chiffrement de g. peut on decoder sans ambiguité

4) le but de cette qustion estde déterminer des conditions sur l'entier a compris entre 1 et 10 pour que le fonction h définie sur V par "h(n) est le reste de la division euclidienne de a^n par 11" permette de chiffrer et déchiffrer correctement un message de 10 caractères. Soit i dans V.

a) montrer que si pour tout i dans V tel que i<10 et a^i n'est pas congru à1 modulo 11,alors la fonction h permet de déchiffrer tout message sans ambiguité

b) montrer qu'ilexiste i dans V tel que i<10 et a^i congru à 1 modulo 11 alors la fonxtion h ne permet pas de déchiffrer un message avec certitude.

c) on suppose que i est le plus petit entier naturel tel i dans V vérifiant a^i congru à 1 modulo 11. en utilisant la division euclidienne de 10 par i prouver que i est un diviseur de 10.

d) quelle condition doit vérifier le nombre a pour permettre le codage et décodage sans ambiguité de tous messages àl'aide de la fonction h? faire la liste de ces nombres

Merci d'avance

[vanhoa]

pour la 4a) et 4b) sert toi de si a congr b et si c congr d alors ac congr bd:

je ne sais pas ce que souhaite ton prof, comme on prend i<10, tu peux les enumerer et le demontrer facilement.
sinon
tu as h(n) qui est le reste de la div eucl de a^n par 11.
donc avec bien sur b dans V

si tu trouves un i tel que alors en faisant tu trouves
ce qui donne le meme reste de la division eucl par 11, donc on ne peut pas decoder, il y a ambiguite

[vanhoa]

ou alors tu supposes que pour avoir ambiguite il faut:
pour tout (a,n,m,b) appartenant a , (k,k’) appartenant a
et
tu l’injecte dans l’expression de et tu divise le tout par et tu auras et ainsi est ton nombre qui congrue 1 [11]

[chtirico]

4a) J'ai essayé d'utiliser la contraposée. Pouvez vous me dire si c'est correct.

Il faut que je montre que si h ne permet pas de déchiffrer tout message sans ambiguité alors il existe un i dansV tel que i<10 et a^i = 1[11]

Si h ne permet pas de déchiffrer tout message sans ambiguité alors il existe k et j dans V avec jdonc a^k – a^j = 0[11]
donc a^j (a^(k-j) – 1) = 0[11]
comme a et 11 sont premiers entre eux alors d'ap le théorème de Gauss a^(k-j) – 1 = 0[11]
donc a^(k-j) =1[11]
En posant i = k-j, i est bien dansV et i <10.
donc a^i =1[11]

4b) je ne sais pas

4c) A vérifier
soit 10 = qi + r avec rD'ap le théorème du petit fermat a^10 = 1[11]
donc a^(qi+r) = 1[11]
donc a^(qi) a^r =1[11]
donc (a^i)^q a^r =1[11]
donc a^r = 1[11]
donc r = 0 car i est le plus ptt élément de V tel que a^i=1[11]
donc 10 = qi
donc i est un diviseur de 10

4d) A vérifier
si on résume les résultats précédents, comme 1, 2 et 5 et 10 sont les seuls diviseurs de 10, il ne faut pas que a,a^2, a^5 et a^10 soient congrus à 1 modulo 11.
un rapide calcul conduit aux valeurs possibles 2, 6, 7 et 8

[vanhoa]

utilise ce que j'ai mis dans mon dernier message pour la 4b)

exemple pour a=3, si tu prends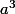 , tu trouveras une ambiguite avec soit tous les 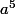, donc ici le 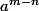est le 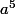(pour 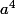ca va etre etc...)

donc pars comme je l'avais fais, soi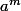t et 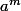sont ambigue, et cela donne 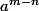congru a 1 [11] (avec m>n)

enfin dsl je fais ca en speed, je suis au taff, mais essaie de partir de cette idee peut etre

j'espere que ca t'auras servi

++

[vanhoa]

lol je viens de lire ce que tu avais mis pour ton 4a)
bah pour ton 4b) c'est tres similaire, c'est dans l'autre sens non? tu pars d'un et tu aboutis a l'ambiguite...