Formule de Taylor-Young

[ludo56]

Bonjour,j'ai décidément un gros problème avec la formule de Taylor-Young.
Il est dit que cette formule a un caractère local:par exemple à l'ordre 1, on a
f(x)=f(a)+f'(a)(x-a)+ et si j'ai bien compris,cette égalité n'est vraie que pour des x proches de a (j'insiste sur "si j'ai bien compris").
Or j'ai pris un exemple:je développe la fonction en 0 à l'ordre 4:

A priori,cette égalité n'est vraie que pour des valeurs de x proches de 0. Et pourtant en tapant sur ma calculette ,je trouve 7,38905... et en remplaçant x par deux dans le develloppement de je trouve quelque chose qui se rapproche de la valeure exacte. Alors le calcul me dit que la formule est vraie pour tout x.Bref,je ne comprends plus rien et votre aide est vraiment la bienvenue!
Merci d'avance.

[Edward]

Ta formule est vrai pour tout x. Cependant, au voisinage de 0 le petit tau de x^4 va faire que tu peux "confondre" exponentielle avec la partie polynomiale du DL. Cette approximation sera d'autant plus précise que tu pousse ton DL loin ou que tu te rapproches de 0.

[ludo56]

D'accord,super c'est précisément la réponse que j'espérais!
Merci

[Ben314]

Tu semble effectivement avoir un petit problème de compréhension de la formule !!!
La "formule" f(x)=f(a)+f'(a)(x-a)+o(x-a) est valable pour tout x du domaine de définition de f, sauf que, dans cette formule, il faut comprendre ce que signifie le "o(x-a)" de la fin.

o(x-a) est une fonction quelconque dont la seule propriétée vraiment connue et que, si on la divise par x-a et que l'on fait tendre x vers a, cela fait 0 (c'est la définition de "o(x-a)").
Cela signifie que o(x-a) est trés petit si x est assez proche de a donc que f(x) est trés proche de f(a)+f'(a)(x-a) lorsque x est proche de a.
Evidement, comme on a (en général) aucune information concernant les valeurs de o(x-a) lorsque x n'est pas proche de a, on ne sait à priori rien concernant l'écart entre f(x) et f(a)+f'(a)(x-a) lorsque x n'est pas proche de a : ça peut être quand même trés petit... ou ne pas l'être !!!

Bon, en plus, en math, utiliser les mots "trés petit" ou "trés proche", ça veut pas dire grand chose si on ne précise pas "à combien prés". C'est (un peu) pour cette raison que toutes les rédactions "propres" utilisent le langage des limites et n'utilisent jamais les mots "proche de" ou "trés petit".


EDIT : Grillé par Edward...
Attention quand même au fait que, si x n'est pas proche de a, de "pousser le D.L plus loin", ça ne marche pas toujours...
Par exemple, le D.L. de ln(1+x), aussi loin qu'on le calcule ne donnera jamais d'approximation de ln(3)=ln(1+2)...

[ludo56]

D'accord,merci pour ces précisions!

[Edward]

Attention quand même au fait que, si x n'est pas proche de a, de "pousser le D.L plus loin", ça ne marche pas toujours...
Par exemple, le D.L. de ln(1+x), aussi loin qu'on le calcule ne donnera jamais d'approximation de ln(3)=ln(1+2)...

Merci en effet pour les précisions ^^

[mathelot]

à propos de Taylor, quelqu'un pourrait m'écriree une formule de Taylor
à n variables de Rn dans Rp avec du calcul symbolique ?

faut élever symboliquement l'opérateur de différentiation à la puissance n
et utiliser les coefficients multinomiaux.. qu'est-ce que cela donne ?

merci

[Ben314]

Rappel : Si est de classe , alors, pour tout ,

est une application linéaire
est une application bilinéaire symétrique
est une application trilinéaire symétrique
.
.
.

[mathelot]

Rappel : Si est de classe , alors, pour tout ,

est une application linéaire
est une application bilinéaire symétrique
est une application trilinéaire symétrique
.
.
.

j'imagine que ,dans l'espace d'arrivée, on travaille composante par composante (de l = 1 à m)

Pour une composante donnée de l'espace d'arrivée,
et pour l'application tri-linéaire par exemple
comme on considère accroissements infinitésimaux
du tuple de départ
on élève le multinome
au cube
en écrivant des dérivations au lieu d'exponentiations.


et on applique le résultat (opérateur linéaire en ,
à destination des applications tri-linéaires), au n_tuple
quand formellement, le terme de la somme correspond à un produit

je ne vois pas trop comment sont fabriqués les coefficients multinomiaux
,style ,
dans la formule ?

merci

[Arkhnor]

Bonjour.

Le polynôme de Taylor à l'ordre n, dans s'écrit, avec des multi-indices :

,

où , , , , et .

Ouf !

[mathelot]

Bonjour.

Le polynôme de Taylor à l'ordre n, dans s'écrit, avec des multi-indices :

,

où , , , , et .

Ouf !

Arkhnor,
pas trop d'accord. A la fin de la ligne , la dérivation par \alpha
est l'exponentiation formelle par
moi, j'écrirai plutôt


de manière que les coefficients , dans le résultat final, soient des entiers et
pas des fractions.

[Arkhnor]

Ce sont des notations standards, utilisées par beaucoup de monde.
Je n'ai rien inventé ...

[mathelot]

Ce sont des notations standards, utilisées par beaucoup de monde.
Je n'ai rien inventé ...

avec la formule telle que tu as l'écrite, on récupère des fractions
comme coeff (avec des dénominateurs différents de 1) :hum:

Comme on différentie, en vrai, les coefficients que l'on doit obtenir au final, sont entiers , pas fractionnaires,c'est ça que j'essaye de t'écrire

relis ta formule, elle donne des fractions. on ne va pas découper les accroissements infinitésimaux, tout de même :mur:

[Ben314]

Sinon, si tu veut reprendre les notations correspondant à :

(je préfère cette formule à celle donnée par Arkhnor du fait qu'elle montre mieux qu'il n'y a aucune différence avec le cas des fonctions d'une seule variable)
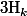
alors, en considérant que les coordonnées des sont , on a :

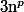
(avec termes dans la somme !!!)
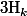
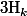
Qui est une aplication linéaire en chacun des et qui est en fait symétrique en les (Théorème de Schwarz)
C'est justement cette symétrie qui permet de regrouper des termes lorsque l'on calcule dans la formule de Taylors
et qui fait apparaitre les fameux coefficients multinomiaux :
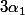
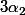
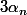
Ils correspondent trés précisément aux nombres de p-uplets tels qu'il y ait d'entre eux égaux à 1, d'entre eux égaux à 2... , d'entre eux égaux à n (avec évidement )


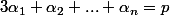
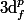
EDIT : Il y a bien des fractions dans le résultat final qui proviennent en fait des avant le dans la formule de Taylors "classique" (i.e. celle en haut de ce post)
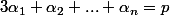
Par contre, si tu utilise les regroupement sus-mentionnée, il apparrait en plus les coeff multinomiaux (avec ) qui, évidement sont entiers (c'est le nombre de p-uplet tels que...)

[mathelot]

ok, je viens de comprendre.

les formules d'Arkhnor et de Ben314 sont exactes toutes les 2.
ce que je contestais (in petto :we: ) , c'est que la formule de Ben314 est théorique, celle d'Arkhnor est pratique (mais on ne voit rien)

je propose la "mienne" , semi-pratique




où la puissance p (p entier, pas multi-entier) est obtenu avec le multinôme

[Arkhnor]

(je préfère cette formule à celle donnée par Arkhnor du fait qu'elle montre mieux qu'il n'y a aucune différence avec le cas des fonctions d'une seule variable)

Et elle se généralise en dimension quelconque, pas nécessairement finie.

Sinon, la présence des fractions vient effectivement du fait que j'ai tout groupé en bloc, mais en groupant par paquets, où chaque paquet correspond à une dérivation de degré , on fait apparaître les coefficients multinomiaux.

Mais je ne vois pas où est l'hérésie dans la présence de coefficients non entiers.
C'est juste un jeu d'écriture ...

[Ben314]

Mais je ne vois pas où est l'hérésie dans la présence de coefficients non entiers.

Je vois pas trop non plus le problème des coeff "pas entier"...

[Arkhnor]

Juste pour le fun, on peut aussi écrire la formule de Leibniz, en multivariables, et dans les deux notations. (multi-indices, et avec les différentielles)

, avec si pour tout i, et

, où désigne répété p fois.

Je trouve les notations multi-indicielles assez élégantes, même si elles cachent un peu la nature des choses