Cet exercice propose une étude du coût, des recettes et du bénéfice de cette opération financière, pendant l'année qui suit sa réalisation.
Les données financières sont exprimées en milliers d'euros (k() et les résultats demandés seront arrondis à 10;)1 près.
Partie A étude du coût
1. Le coût de l'opération financière s'élève la fin du 1ermois à 50 k et à la fin du 2e mois à 46 k.
Calculer la diminution en pourcentage du coût entre le premier et le deuxième
mois.
2. On note un le coût exprimé en kg de l'opération financière à la fin du n-ième
mois (1 n 12), ainsi u0 = 50 et u1 = 46.
On admet que (un) est une suite géométrique de raison 0,92.
Calculer u11.
3. En fait le coût mensuel de l'opération financière suit une évolution légèrement différente et peut êtremodélisé par la fonction f définie sur [1 ; 12] par :
f (t )= 108 / 1+e0,15t
On admet que f (t ) représente le coût mensuel, exprimé en k(, comptabilisé
à la fin du t -ième mois.
a. Calculer f
(t ), pour tout t appartenant à l'intervalle [1 ; 12]. En déduirele sens de variation de f sur l'intervalle [1 ; 12].
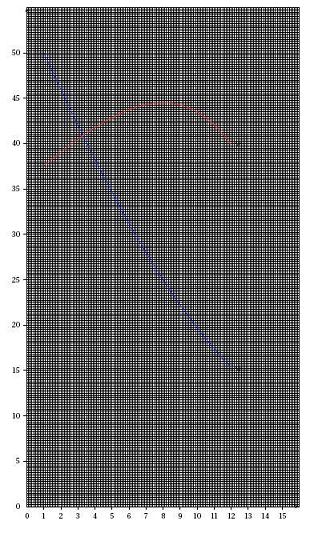
b. En annexe, deux courbes sont tracées. L'une représente la fonction f .
La reconnaître ; expliquer.
Mes réponses:
1/ La diminution en pourcentage du coût entre le premier et le deuxième mois correspond à la formule suivante:
t= (y2 - y1 / y1) * 100 avec y2 en valeur d'arrivée et y1 en valeur de départ
t= (46 - 50 / 50) * 100
t= -8 %
La diminution est donc de -8 %
2/ On a (Un) une suite géométrique de premier terme u0=50 et de raison q=0,92
u11= u0 * q^11
u11= 50 * 0,92^11
u11= 20 (arrondis à 10^-1)
3/
a.
f(t) = 108 / 1+e0,15t sur [1,12]
f(t) est de la forme 1/u
Ainsi, f'(t) = -u'/u² où u=1+e0,15t et u'=0,15t e0,15t
f'(t) = -0,15t e0,15t / (1+e0,15t)²
D'une part (1+ e0,15t)² > 0 car un carré est toujours positif.
D'autre part, pour tout nombre réel de a, e^a > 0 donc e0,15t > 0
Or, -15t < 0 donc f'(t) < 0 sur [1,12]
La fonction f est donc strictement décroissante sur [1,12]
b.
C'est la courbe C' (la bleu sur le schéma) qui représente la fonction f car elle est strictement croissante sur [1,12] tandis que la courbe C(la rouge) elle est croissante puis décroissante.
Voila, j'aimerais savoir si mes résultats sont correctes mais surtout si ma rédaction est bonne car ma prof est très pointilleuse à ce niveau là.
Désolé pour la qualité du schéma.
Merci pour tous.
