Les mathematiques quand tu nous tiens .............

par **matlab** » 28 Mar 2010, 00:11

Bonjour à tous (Oui vous allez dire un petit nouveau premier post et il demande de l'aide -_-!Mais je suis au bord d'un gouffre .... Mon DM de math:) )

ma question et très simple pouvez vous m'aider pour ce devoir de math ?

toute les aides sont les bien venu pour tout les exercies !

Merci d'avance a vous tous

par **sniperamine** » 28 Mar 2010, 01:36

Bonsoir , pour le J1 par exemple tu peux essayer de calculer la dérivée de la fonction (-xcos(ln(x))) et de la fonction ( xsin(ln(x)) ) et conclure !! pour le premier exercice tu peux utiliser les techniques de réduction en éléments simples , de l'intégration par parties ...

par **girdav** » 28 Mar 2010, 09:43

Bonjour,
pour le troisième exercice il faut regarder le problème en

. Pour cela, on peut chercher un équivalent de la fonction à intégrer que sera une fonction puissance.

par **matlab** » 28 Mar 2010, 10:23

Tout d'abord merci pour vos réponse ! mais je n'ai pas tres bien compris le J1 ??
pourrais tu m'expliquer stp ?

par **ffpower** » 28 Mar 2010, 10:41

Pour I1, on peut soit s en sortir en faisant une double intégration par parties, soit ecrire les sinus comme partie imaginaire d'une expo ( mais il faut être a l aise avec les fonctions a valeurs complexes pour cette methode )

Pour J1, plutot qu'essayer d'intuiter la forme du résultat à l'avance, je proposerais plutôt de faire un changement de variables t=ln(x)

par **matlab** » 28 Mar 2010, 14:45

Hum j'essaie de puis avant avec le changement de variable pour le 2) mais j'y arrive pas quelqu'un y voit la lumière ?

par **girdav** » 28 Mar 2010, 14:47

Pour

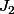
tu peux faire une intégration par parties avec

et

. En refaisant la même chose dans l'intégrale qui en découlera on devrait avoir un truc sympa.

par **matlab** » 28 Mar 2010, 14:50

Tu veux dire pour J1 , je mis met de suite pour voir si la lumière des maths viens !

par **sniperamine** » 28 Mar 2010, 15:30

ffpower a écrit:Pour I1, on peut soit s en sortir en faisant une double intégration par parties, soit ecrire les sinus comme partie imaginaire d'une expo ( mais il faut être a l aise avec les fonctions a valeurs complexes pour cette methode )

Pour J1, plutot qu'essayer d'intuiter la forme du résultat à l'avance, je proposerais plutôt de faire un changement de variables t=ln(x)

mais bon si on peut "intuiter" le résultat c'est mieux je crois lol

par **ffpower** » 28 Mar 2010, 16:12

Une autre méthode encore pour J1 est de dire que l'intégrande est la partie imaginaire de e^{i*ln(x)}=x^i, et une primitive de cette derniere c'est x^{i+1}/(i+1)

par **matlab** » 28 Mar 2010, 18:16

Dsl , j'ai le cerveau qui fond ...

j'ai bien compris pour J1 ,
pour I1 je trouve :

mais pour I2 c'est le flou totale

par **ffpower** » 28 Mar 2010, 19:35

Pour I2, faut juste mettre le trinome du dénominateur sous forme canonique (x+a)²+b. Apres ca dépend du signe de b..

Les mathematiques quand tu nous tiens .............

Les mathematiques quand tu nous tiens .............

Qui est en ligne