Bonsoir bonsoir ! :happy2:
J'ai un petit , non en fait des gros soucis concernant cet exercice de maths...
J'espère que vous pourrez me venir en aide... et je remercie d'avance déjà tous ceux qui ont rien que le courage de lire ce post et de me consacrer un peu de temps!
Une balle est lâchée d'une hauteur d'un mètre.Quand elle rebondit sur le sol, le nouveau rebond a une hauteur égale à la moitié du précèdent rebond.
On Désigne hn la hauteur du énième rebond et on pose h0=1
On me demande de montrer que la suite hn est géométrique et de calculer hn en fonction de n.
Pour qu'une suite soit géométrique il faut que Hn+1=q Hn
Hn=H0*Q^n
Hn=(1/2)^n
On admets ensuite qu'un rebond dont la hauteur est inférieur a 1mm ,'est pas perceptible à l'il nu.On me demande alors de déterminer le nombre de rebonds perceptibles à l'il nu à la calculatrice.
J'ai trouvé que 9 rebonds sont perceptibles a l'oeil nu en résolvant à la calculatrice.
on designe par dn la distance parcourue par la balle depuis son lâcher jusqu'à ce qu'elle ait rebondi n fois.
On me demande de calculer dn en fonction de n et de déterminer la limite de cette suite.
Dn=H0+2H1+2H2.....+2Hn
Dn=( 1-q^(n+1))/( 1-q) )
Sauf que je coince un peu pour le mettre en application et donc pour trouver la limite..
On admet que le temps tn mis par la balle pour parcourir hn du énième rebond , à la descente comme a la montée est donnée par la formule :
tn= racine de(hn/4.9)
Monter que la suite (tn) est géométrique et calculer tn en fonction de n.
- tn+1=k*tn (je supposes)
- tn= t0*q^n
Soit Tn le temps mis par la balle pour effectuer les n premiers rebonds.
Calculer Tn en fonction de n.
Pendant combien de temps de temps voit on rebondir la balle?
Calculer la limite de la suite (Tn).
Découragée des maths...vous êtes je penses mon seul espoir!
Une balle qui rebonsit...suites!
4 messages
- Page 1 sur 1
mejdane a écrit:pour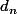
on a-h_0)
et je pense que la calculer ainsi que sa limite est une chose classique
Bonjour, dessolée pour le retard de réponse!
Est ce que je peux faire aussi:
Soit Dn = h0+2h1+2h2....+2hn h0=1
Je dois calculer dn en fonction de n et je dois trouver la limite de cette suite ..
J'ai fais Dn est une suite géométrique de raison 2
donc S= h0* (1-2^(n+1)/ 1-2)= h0*2^(n+1)+1= 2^(n+1)+1
lim =+infini
n tend vers + l'infini :mur:
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
