Groupes

[kazeriahm]

Bonjour a tous,

j'aimerais de l'aide sur cette question

dans le groupe diedral d'ordre 8 G on definit le sous groupe H de G engendre par <(1,2)(3,4),(1,3)(2,4)>. On me demande de montrer que H est normal dans G.

Est-ce que

1) je dois montrer a la main que pour tout g dans G, gH=Hg (ou encore g^-1Hg=H) ?
2) il y a une methode astucieuse qui permet d'eviter ce genre de calcul ?

Si c'est l'option numero 1, alors il suffit de verifier que c'est vrai pour une famille de generateurs de G, donc il suffit de verifier que c'est vrai pour deux elements de G mais ca implique de calculer tous les elements de H, etc... Enfin bref je suis sur qu'il y a beaucoup plus astucieux mais je n'ai pas l'habitude de ce genre d'exo.

Ensuite on me demande d'exhiber deux groupes K1 et K2 de H tels que K1 soit normal dans G mais pas K2 et pour finir on me demande l'ordre du coeur de K2 dans G.

Donc si vous pouvez m'aider pour la premiere partie, peut-etre que ca m'ouvrira les yeux sur la deuxieme...

Merci d'avance.

[skilveg]

Bonjour,

Les deux méthodes sont possibles:

1) Vérifier que le sous-groupe est stable par conjugaison ne demande pas tant de calcul que ça (on n'a que 4 éléments à tester puisqu'on sait déjà que c'est un sous-groupe).

2) Tu peux te servir du résultat suivant (à (re-)démontrer): si est un sous-groupe d'ordre d'un groupe d'ordre , alors est distingué.

Une troisième façon de faire serait de voir comme un noyau, à creuser... (Par exemple on a un morphisme de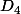 dans 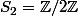puisque tout élément de agit sur les diagonales d'un carré, et on peut voir que le noyau est exactement ton sous-groupe.)

Sinon, qu'est-ce que tu appelles "coeur" d'un sous-groupe?

[kazeriahm]

Merci pour ta réponse, en fait comme souvent je me rends compte que je poste en n'ayant pas assez réfléchi au problème. Sinon le terme "coeur" je l'ai traduit de l'anglais "core" (je suis des cours en Nouvelle-Zélande), la définition est donnée ici (première définition)
http://en.wikipedia.org/wiki/Core_%28group%29

[kazeriahm]

Ok donc juste pour checker

H admet trois sous groupes d'ordre 2, tous normaux dans H (conséquence du résultat que tu m'as donné d'ailleurs). Seul l'un d'entre eux (celui qui contient la rotation) est normal dans G, et du coup l'ordre du coeur (le coeur de H dans G étant le plus grand sous groupe normal dans G inclus dans H) de ces deux groupes est 1. All right?

[kazeriahm]

Deux autres questions issues de la même planche :

(1) N est un sous groupe normal d'ordre fini de G, H est un sous groupe de G d'indice fini. On suppose que pgcd(|N|,|G:H|)=1. Montrer que N est inclus dans H.

(2) N est sous groupe normal d'indice fini dans G. H est un sous groupe de G d'ordre fini. On suppose pgcd(|H|,|G:N|)=1. Montrer que H est inclus dans N.

Je suis un peu sec là dessus... Pour la (1) j'ai essayé de regarder HN qui est un sous groupe de G, et de montrer qu'il est égal à H avec l'argument pgcd portant sur le nombre de classes de H dans G et sur l'ordre de N mais rien de bien concluant. Quelqu'un peut-il me mettre sur la voie ?

Merci d'avance

[Doraki]

il faut voir que grace à la normalité de N ou de H, N opère transitivement sur l'ensemble des classes de H dans NH :

[NH:H] = #{xH, x dans NH}
Mais N est normal dans G (donc dans NH), donc tout élément x de NH s'écrit x = nh avec n dans N et h dans H. (et pareil si c'est H qui est normal dans G)
Donc [NH:H] = #{nH, n dans N}.

A partir de là c'est plus très dur de montrer que [NH:H] divise |N|

[kazeriahm]

Mais N est normal dans G (donc dans NH), donc tout élément x de NH s'écrit x = nh avec n dans N et h dans H.

En quoi est-ce que la décomposition x=nh pour x dans NH est une conséquence de la normalité de N ? Je veux dire N normal implique que NH est un (sous) groupe mais par définition x=nh non ? Donc par définition {xH, x dans NH}={nH, n dans H} non ?

[Doraki]

Je pensais que par NH tu désignais le sous-groupe engendré par N et H.

[kazeriahm]

Ok et donc si je montre que [NH:H] divise |N|, je suppose qu'il est clair (même si ca ne me saute pas encore aux yeux) que [NH:H] divise [G:H] donc du coup NH=H ?

[Doraki]

Oui, [G:H] = [G:NH] * [NH:H].
on se retrouve avec [NH:H] premier avec [G:H] donc [NH:H] = 1.

[kazeriahm]

Merci beaucoup. Et donc la deuxieme question est exactement la meme en fait, le fait qu'on transpose l'hypothese de normalite sur le groupe d'index fini ne change rien, puisque NH est toujours un groupe. All right?

[miikou]

salut si g^-1 * h *g est dans H alors c'est bon, linclusion suffit par besoin de montrer legalité