Inéquation différentielle

par **Nightmare** » 15 Mar 2010, 15:31

Salut :happy3:

Sauriez-vous trouver les applications dérivables

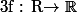
telles que

?

:happy3:

par **bg38** » 15 Mar 2010, 16:23

lut.
ben il suffit de résoudre l' équa diff;
f²+2f'+(f')²-m=0
Avec m

[-

; 0]

non?

par **Nightmare** » 15 Mar 2010, 16:27

Euh... Encore faudrait-il montrer avant que f²+2f'+(f')² est constante !

par **bg38** » 15 Mar 2010, 16:32

oups j'avais oublié :briques:

par **Ben314** » 15 Mar 2010, 18:07

Salut,
L'inéquation s'écrit

donc

et

:

est décroissante sur

.
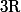
S'il existait un

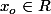
tel que

alors

donc

ce qui, en faisant tendre

vers -oo,contredirait le fait que

est majorée par 1.

Conclusion :

est identiquement nulle

par **Nightmare** » 15 Mar 2010, 18:19

Ca me va :happy3:

Joli !

P-S : Je sais pas pourquoi, mais tu me démoralises à chaque fois que tu postes une solution, toujours plus simple que la mienne. Mais comme toi dire, toi prof, moi étudiant :lol3:

par **grikor** » 15 Mar 2010, 18:26

bonsoir.
je trouve (f'+1)²+f²<=1;

(f'+1)²-1<=-f²<=0; (f'+1)²-1<=0;

(f'+1)²<=1; (f'+1)<=+-1;

f'<=0 et f'<=-2;

f'<=-2; f<=c-2x

par **Nightmare** » 15 Mar 2010, 18:32

grikor a écrit:bonsoir.

(f'+1)²<=1; (f'+1)<=+-1;

Déjà ça, ça ne me va pas :lol3:

par **Ben314** » 15 Mar 2010, 18:55

Nightmare a écrit:Mais comme toi dire, toi prof, moi étudiant :lol3:

De plus, si moi y'en a pas trouver joulie solution, moi y'en a rien poster du tout....
Par exemple, ici, j'était parti avec du plus compliqué au départ en écrivant des inéquations de la forme f'*(fonction_de_f)>-1 (ou <-1) et en intégrant...

par **Nightmare** » 15 Mar 2010, 18:57

Ah ah, j'étais parti sur ce genre d'idée aussi. C'est quand j'ai vu que f était décroissante que tout s'est "arrangé".

Inéquation différentielle

inéquation différentielle

Qui est en ligne