Forme linéaire
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 09 Mar 2010, 18:10
par barbu23 » 09 Mar 2010, 18:10
Bonjour : :happy3:
Soit

un

- espace vectoriel de dimension finie.
Soit :

une forme linéaire.
Par definition :

:

 = \displaystyle \sum_{i=1,...,n} \varphi(e_{i}) e_{i}^{*}(x) $)
avec :
 = x_{i} $)
Par conséquent :
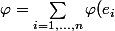 e_{i}^{*} $)
Et donc :
 = = = \displaystyle \sum_{i,j=1,...,n} \varphi(e_{i}) x_{i} = \displaystyle \sum_{i,j=1,...,n} \varphi(e_{i}) x_{j} \delta_{i}^{j} $)
Ce qui caracterise les formes linéaires, ce sont :
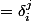
.
Je voudrais savoir comment s'appelle
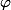
dans le cas où :

.
Désolé si la question vous semble stupide, mais je suis un peu perdu là !
Merci d'avance ! :happy3:

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 09 Mar 2010, 18:12
par Ben314 » 09 Mar 2010, 18:12
Ca s'appelle... qu'on s'est gourré quelque part, vu que la formule :
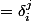
Eh bien c'est
la définition des formes linéaires

...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 09 Mar 2010, 18:14
par barbu23 » 09 Mar 2010, 18:14
Oui, mais là c'est different, j'ai dit que

mais pas :
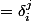
:happy3:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 09 Mar 2010, 18:16
par barbu23 » 09 Mar 2010, 18:16
ça n'existe pas ? ou bien c'est une forme bilinéaire tout simplement ? :happy3:
-
gnarfk
- Membre Naturel
- Messages: 11
- Enregistré le: 14 Fév 2009, 23:44
-
 par gnarfk » 09 Mar 2010, 19:28
par gnarfk » 09 Mar 2010, 19:28
Non .
tes autres trucs sont des formes linéaires de ta deuxième variable aussi. c'est juste que le phi particulier qui permet d'écrire sous cette forme en delta_i,j est unique , mais rien n'interdit d'écrire la forme autrement.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 09 Mar 2010, 19:36
par barbu23 » 09 Mar 2010, 19:36
Le truc qui me gène est ce qui suit :
Pourquoi dit - on que :
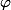
tel que
 = $)
est une forme linéaire ( c'est à dire, une application ) alors, qu'elle est simplement un vecteur comme

? :happy3:
Si on se permet d'écrire les choses de cette manière, on devrait aussi dire que :

est une forme linéaire et l'ecrire comme ça :
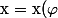 = \displaystyle \sum_{i=1,...,n} x_{i} e_{i}(\varphi) = \displaystyle \sum_{i=1,...,n} x_{i} e_{i} $)
Et donc, aucune difference entre un vecteur et une forme linéaire ! :happy3:
-
gnarfk
- Membre Naturel
- Messages: 11
- Enregistré le: 14 Fév 2009, 23:44
-
 par gnarfk » 09 Mar 2010, 19:45
par gnarfk » 09 Mar 2010, 19:45
c'est ce qu'on appelle la dualité entre les vecteurs et les formes linéaires.
mais personnellement , quand je dis que phi est tel que phi(x) =
, pour moi phi est un vecteur (qui a un nom particulier : le gradient). ensuite on peut s'amuser à le considerer comme une application , et une application comme un vecteur , c'est juste la dualité entre l'espace et les formes linéaires sur lui.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 09 Mar 2010, 19:57
par barbu23 » 09 Mar 2010, 19:57
Oui, voilà , Merci ! :happy3:
Parceque en dimension finie :

s'identifie à son bidual

:happy3:
-
mathofil
- Messages: 5
- Enregistré le: 29 Mar 2015, 13:56
-
 par mathofil » 29 Mar 2015, 21:07
par mathofil » 29 Mar 2015, 21:07
barbu23 a écrit:Bonjour : :happy3:
Soit

un

- espace vectoriel de dimension finie.
Soit :

une forme linéaire.
Par definition :

:

 = \displaystyle \sum_{i=1,...,n} \varphi(e_{i}) e_{i}^{*}(x) $)
avec :
 = x_{i} $)
Par conséquent :
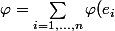 e_{i}^{*} $)
Et donc :
 = = = \displaystyle \sum_{i,j=1,...,n} \varphi(e_{i}) x_{i} = \displaystyle \sum_{i,j=1,...,n} \varphi(e_{i}) x_{j} \delta_{i}^{j} $)
Ce qui caracterise les formes linéaires, ce sont :
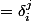
.
Je voudrais savoir comment s'appelle
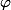
dans le cas où :

.
Désolé si la question vous semble stupide, mais je suis un peu perdu là !
Merci d'avance ! :happy3:
vu le type de e_i (base orthonormale) ; tu ne pourras jamais avoir un resultat autre que 0 ou 1
c est le principe de projection orthogonale
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités
