Pour

, il suffit de faire disparaitre une variable de ton système à deux equation ( Par exemple, on veut faire disparaitre

, donc, tu multiplies la deuxième eqsuation par

ensuite, tu soustrais la première equation de la seconde , tu auras une equation à deux variables, tu ecris l'une en fonction de l'autre , tu obtiens par exemple :
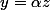
, tu montes à la première equation du système, tu remplaces

par sa valeur :
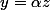
, et tu obtiens une equation à deux variables

et

, et tu l'ecris comme ça :

!
Et voilà ! L'ensemble des solution du système et le triplet :
 = (z,\alpha z, \beta z) = z (1,\alpha ,\beta) $)
, en rempalcant

par
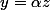
, et

par

dans le triplet ! et voilà ! l'ensemble des solutions est :
 $)
.
:happy3:
