Dérivées, minimum, produit scalaire

par **tipie51** » 27 Fév 2010, 21:02

Bonjour,
J'ai un problème dans un exercice ...
" Soit (O;i;j) un repere orthonormé du plan. On appelle D la droite d'équation y = -2x+3
A le point de coordonnées ( -3;-1 ). On prend un point M quelconque sur D.
1. Exprimer AM² en fonction de x
J'ai noté :
AM² = (xM - xA)² + (yM-yA)² = (x-3)² + (y+1)² = x²+y²+6x+2y+10
Est ce bon ?
2. Démontrer que AM² admet un minimum et trouver les coordonnées de Mo le point correspondant.
3. Prouver, en utilisant le produit scalaire, que Mo est le projeté orthogonal de A sur D.

J'aurais besoin d'aide pour les question 2 et 3. Admettre un minimum, c'est quoi ? comment trouver ?
Merci :stupid_in

par **Zweig** » 27 Fév 2010, 21:06

Salut,

Je n'ai pas vérifié tes calculs mais s'ils sont juste alors la distance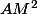

peut-être considérée comme une fonction ne dépendant que de

:

en utilisant le fait que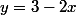

Ainsi, après développement et simplifications :

Il te faut trouver la ou les valeur(s) de

telle(s) que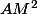

atteigne son minimum (question 2)).

par **Zweig** » 27 Fév 2010, 21:09

Pour déterminer le minimum soit tu utilises les dérivées (si tu les as vues), soit tu peux aussi remarquer que

par **tipie51** » 27 Fév 2010, 21:12

Merci Mais peux tu me dire si c'est juste sinon je vais droit dans le mur ...
Et qu'est ce que je fais après avoir étudier la dérivée ?

par **tipie51** » 27 Fév 2010, 21:40

Peut on m'aider s'il vous plait ?

par **oscar** » 27 Fév 2010, 22:06

La dérivée de 5x² -10x +25 est 10x -10 ( formul (x^m)' = mx^ (m-1)
sa racine x = 10
Tu obtiens ainsi le sommet pour x= soit 10
f( 100) = 5*10² -10*10 +25=..

Dérivées, minimum, produit scalaire

dérivées, minimum, produit scalaire

Qui est en ligne