Equivalents et équations différentielles

[Skullkid]

Bonjour, j'aimerais savoir si - sous certaines hypothèses - il existe un énoncé du genre : Si 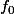est solution de l'équation différentielle et si f est une fonction qui vérifie , alors .

En ce qui me concerne j'en aurais besoin pour .

[JeanJ]

Bonjour,

Si j'ai bien lu, l'équation est :
y''-y/x²=0
C'est une équation différentielle linéaire sans second membre, donc l'une des plus simples parmi les plus simples.
On cherche des solutions de la forme y=x^p
p(p-1)-1 = 0
dont les racines sont :
p1 = (1+sqrt(5))/2
p2 = (1-sqrt(5))/2
La solution générale de l'équa. dif. est :
y = A*x^p1 +B*x^p2
avec A et B des constantes quelconques.

[Skullkid]

Oui, je sais résoudre l'équation en question. Mon problème c'est que j'ai une fonction inconnue f qui vérifie , et j'aimerais savoir s'il y a un moyen de montrer que f est équivalente à une solution de l'équation.

[Ben314]

Salut,
A moins que je ne soit totalement couillon, ta question semble être :
.
Ce qui, clairement ne marche pas si tu n'as pas d'hypothèses concernant le lien entre et ainsi qu'entre et

Si tu préfère, en revenant à la notion d'équa diff., même si tu avais deux égalitées : et , tu ne pourrais pas en déduire grand chose comme lien entre f_o et f si tu n'as pas les mêmes conditions initiales...

[Ben314]

Si ton problème est de savoir si f est équivalente à UNE DES solutions de l'équation, je suppose que ton 'a' vaut 0 (??) ou bien que f(a)=0 (??)
(Car sinon, deux fonctions f et fo telle que f(a)=fo(a) [non nul] sont forcément équivalentes au voisinage de a)
Troisième possibilité, ce n'est pas l'équivalence (au sens quotient tend vers 1) qui t'interesse mais quelque chose de plus précis (par exemple le même D.L. à l'ordre 2)

En résumé, précise un peu la question...

[Skullkid]

Oui Ben, c'est bien ça ma question. En fait je ne cherche pas un équivalent "précis" : l'équation est de solutions les 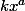. Est-ce qu'il y a un moyen de démontrer que si f vérifie , alors il existe k tel que ? Je ne cherche pas à connaître la valeur de k (donc je ne m'intéresse pas aux conditions initiales).

On ne peut pas intégrer les équivalents, mais on peut intégrer les DL, donc je me disais qu'il y avait peut-être des hypothèses qui feraient que...

Edit : désolé pour avoir été un peu flou, c'est bien l'équivalence qui m'intéresse, pas les termes suivants du DL.

[Ben314]

Perso, je suis pas super à l'aise avec les équa diff. et avec les problèmes de "sensibilité" des solutions si on fait varier l'équation [on peut voir ta fonction f comme une vrai soluce d'une équa diff y''(x)=phi(x)y(x) où la fonction phi est équivalente en 0 à x->a(a-1)/x²]

Là ou en plus ça risque d'être coton, c'est que 0 est un pôle (je sais pas si c'est comme ça qu'on dit) de l'équa diff de départ donc je ne pense pas (???) qu'il y ait de "gros théorèmes" qui vont s'appliquer "direct"...

Bon, déjà, si 0x^(1-a) est elle aussi prolongeable en 0, dont ta fonction f pourrait avoir pour équivalent x^(1-a).

Donc mes questions suivante sont :
1) Sait tu dans quel partie de R : ]0,1[ ou ]-oo,0[u]1,oo[ est situé 'a' (je voterais bien pour la deuxième, là ou une seule des "deux" solutions de base est prolongeable en 0) ?
2) Suppose tu ta fonction f définie, continue, dérivable... sur [0,oo[ (y compris en 0) ? (je pense que oui pour être sûr que f n'est pas proche de la deuxième solution... )

P.S. Ces questions ne m'apparaissent pas vraiment comme des "imprécisions" de ton énoncé, mais comme un "cernage" progressif du problème.
De plus, une fois le problème "bien cerné", je suis trés loin d'être sûr que je (on) puisse y apporter une réponse... Et je n'ais pas d'intuition trés claire, doit on chercher une preuve... ou un contre exemple...

[Skullkid]

Mon a est dans (on peut peut-être traiter le cas a = 1/2 à part ?), en 0 je sais juste que f est continue. Par contre elle est sur .

Edit : plus précisément, f est de la forme avec g qui est sur .

[Ben314]

Si je me suis pas gourré, ton hypothèse devient dans ce contexte :

S'il existe un entier n tel que , il me semble que c'est gagné, par contre, si pour tout entier n on a (du type g(x)=exp(-1/x) pour x>0) alors ça ne me parrait pas clair du tout.

P.S. Il faut que j'aille faire à bouffer : j'essaye d'y réfléchir en épluchant les patates, mais sans papier, c'est pas gagné...

P.S.2 Dans le cas a=1/2, les deux soluces "de base" de l'équa diff sont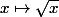 et dont seule la première et du type avec g donc je ne pense pas que a=1/2 représente un cas particulier.