Suites numériques (1ere S)
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
GIGrubby
- Membre Naturel
- Messages: 13
- Enregistré le: 26 Sep 2009, 13:48
-
 par GIGrubby » 17 Fév 2010, 07:55
par GIGrubby » 17 Fév 2010, 07:55
Bonjour,
je coince sur un tout petit exercice.
(Un) est une suite croissante. (Vn) est la suite définie par Vn=1/n * (U1+U2+...+Un), pour tout nN*. Démontrez que (Vn) est croissante
J'ai déjà essayé plusieurs méthodes qui n'aboutissent a rien. Mon problème c'est que on peut pas exprimer U1+...Un d'une autre facon vu que la suite n'est ni géométrique ni arithmétique.
Donc si quelqu'un pouvait m'éclairer. merci
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 17 Fév 2010, 10:00
par Sylviel » 17 Fév 2010, 10:00
Ce que tu veux montrer c'est que la moyenne d'une suite croissante est croissante. Essaie de comparer Un à Vn, puis Vn+1 à Vn. Il y aplein d'arguments possibles, moi je trouve que l'utilisation de la notion de barycentre, si tu connais, est assez classe ici.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
GIGrubby
- Membre Naturel
- Messages: 13
- Enregistré le: 26 Sep 2009, 13:48
-
 par GIGrubby » 17 Fév 2010, 12:09
par GIGrubby » 17 Fév 2010, 12:09
J'ai déjà essayé de comparer Vn+1 à Vn en divisant et en soustrayant mais j'arrive a rien.
Comparer Un à Vn je vois pas non plus comment faire et quel en est l'interet ?
Le barycentre je connais pour des points mais pour des suites je connais pas.
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 17 Fév 2010, 12:15
par Sylviel » 17 Fév 2010, 12:15
Je parle bien du barycentre de points (sur une droite en l'occurence), mais ça viendra plus tard, et ce n'est pas nécessaire de le voir comme cela.
Pour le moment essaie de réfléchir à ce que signifie Vn pour Un, et à comparer Un et Vn. Ensuite on verra pour Vn et Vn+1.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
GIGrubby
- Membre Naturel
- Messages: 13
- Enregistré le: 26 Sep 2009, 13:48
-
 par GIGrubby » 17 Fév 2010, 13:16
par GIGrubby » 17 Fév 2010, 13:16
Vn est la moyenne des U de U1 à Un.
et j'ai trouvé que


etc...
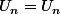
On additionne

/n < U_n)
car n est positif, non nul

Et après pour V_(n+1) et V_n ??
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 17 Fév 2010, 15:31
par Sylviel » 17 Fév 2010, 15:31
Bien ! Exprimes Vn+1 en fonction de Un+1 et Vn
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
GIGrubby
- Membre Naturel
- Messages: 13
- Enregistré le: 26 Sep 2009, 13:48
-
 par GIGrubby » 17 Fév 2010, 16:08
par GIGrubby » 17 Fév 2010, 16:08
= (U_1+ ... +U_(n+1) ) / (n+1) = ( (U_1+..U_n) / n * n + U_(n+1)) / (n+1)<br /><br />=( V_n * n + U_(n+1) )/ (n+1))
Voilà mais je vois pas quoi faire après

-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 17 Fév 2010, 17:14
par Sylviel » 17 Fév 2010, 17:14
et bien ton objectif est de montrer que Vn+1 > Vn
Donc tu as une expression de Vn+1, utilise la croissance de Un, puis la comparaison que tu as faite pour retomber sur Vn.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
GIGrubby
- Membre Naturel
- Messages: 13
- Enregistré le: 26 Sep 2009, 13:48
-
 par GIGrubby » 17 Fév 2010, 17:20
par GIGrubby » 17 Fév 2010, 17:20
désolé mais je comprend pas vraiment ce que tu veux dire.
Je sais pas d'où partir là
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 17 Fév 2010, 17:21
par Sylviel » 17 Fév 2010, 17:21
tu as Vn+1=

minore cette expression en utilisant la croissance de la suite Un. Puis en utilisant la comparaison du début. Conclut.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
GIGrubby
- Membre Naturel
- Messages: 13
- Enregistré le: 26 Sep 2009, 13:48
-
 par GIGrubby » 17 Fév 2010, 17:34
par GIGrubby » 17 Fév 2010, 17:34
minore cette expression = ?
Je la réduit ? et je comprend pas "en utilisant la croissance de (Un)"
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 17 Fév 2010, 19:39
par Sylviel » 17 Fév 2010, 19:39
Et bien minorer Vn+1 signifie trouver quelque chose de plus petit que Vn+1. La croissance de Un signifie que Un+1>=Un...
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
GIGrubby
- Membre Naturel
- Messages: 13
- Enregistré le: 26 Sep 2009, 13:48
-
 par GIGrubby » 18 Fév 2010, 07:18
par GIGrubby » 18 Fév 2010, 07:18
Ok je pense avoir trouver.
(Un) est croissante donc :

donc U

d'où
 / n+1 < (nV_n + U_n_+_1) / (n+1))

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 89 invités
