Resolution d'équations différentielles de degré 1

[grego]

équation différentielle : y+y'=sinx

Je la résouds comme une équation différentielle linéaire.
Recherche de la solution homogène : y+y'=0
Y= e^-x * constante
Recherche de la solution particulière :
y=Ke^-x
y'=K'e^-x - Ke^-x
On remplace dans la solution de départ :
K'e^-x = sinx
K'= sinx * e^x

Mais je n'arrive pas à trouver une primitive de sinx * e^x. Je tourne en boucle.
Pouvez-vous m'aider?


équation différentielle : y'=(2x+y²)/xy
C'est une équation différentielle de Bernoulli:
Z=y^1-2
Z=y^-1
Z=1/y
y=1/Z
y'=-Z'/Z²
Je remplace dans l'expression de départ et j'arrive a : Z'/Zx + 1/Z² = -2x
Recherche de la solution homogène car on est revenu a un ED linéaire:
Z'/Zx + 1/Z² = 0
Z'/Zx = -1/Z²
ZZ'/x = -1
ZZ' = -x

Et je suis bloqué ici. Pouvez vous m'aider?
Merci

[busard_des_roseaux]

Bs,


deux méthodes pour primitiver

i) poser

la partie Imaginaire et la primitivation sont R-linéaires et commutent

ii) intégrer deux fois par parties pour retomber sur la même intégrale avec un signe - dans l'autre membre

iii) chercher par coeff indéterminés

trouver l'erreur :we:

pour la (2)
zz' est la dérivée de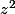 modulo un facteur multiplicatif

[grego]

Pour l'intégrale de sinx e^x:
S: représente l'intégrale
J'ai intégré 2 fois : et je tombe sur sinx e^x - cosx e^x + S (sinx e^x)

Mais je ne vois pas ce qui faut faire après.

[busard_des_roseaux]

il y a une erreur de signe.

tu dois trouver -S pour résoudre une équation en 2S

[grego]

Oui désolé
c'est e^x - cosx e^x - S (sinx e^x)

Mais après je vois pas la méthode pour résoudre une équation en 2S

[grego]

ah je crois que j'ai trouvé :
donc sinx e^x - cosx e^x - S (sinx e^x) = 0
S (sinx e^x) = sinx e^x - cosx e^x
S (sinx e^x) = e^x ( sinx - cosx) ??

[busard_des_roseaux]

c'est la primitive l'inconnue ... l'équation est du 1er degré

[busard_des_roseaux]

pas 0 mais 2S .......................

[busard_des_roseaux]

il faut primitiver



1ère méthode: les nombres complexes




c'est linéaire et ça commute
on vient de primitiver l'exponentielle
e^x est réel,sort de la partie imaginaire
forme trigo de 1+i
le réel sort de la partie imaginaire
calcul de la partie imaginaire



2ème méthode: 2 intégrations par parties
on intégre l'exponentielle tout le temps


attention, il y a trois signes moins




conclusion: ici , l'intégration par parties est simple
car une primitive de x --> e^x est un jeu d'enfant.

Le calcul avec les complexes est très intéressant à étudier et à comprendre pour progresser

bon courage ! :++: