Equation differentielle

[MathematicienPoche]

Bonjour,

j'ai une équation différentielle assez simple à résoudre: y' = y/(y + t) .

On ne peut pas trouver de facteur intégrant, je ne peux pas séparer les variables. J'ai pensé à la méthode z = y/t, mais ca ne mene nulpart. Alors, comment faire?

merci.

[Ben314]

Salut,
J'ai l'impression que ça marche en posant z=y/(y + t)
(mais me demande pas pourquoi ça marche...)

[JeanJ]

y' = dy/dt = y/(y + t)
dt/dy = (y+t)/y
La fonction à calculer est t(y)
y (dt/dy) -t = y
ED homogène : y (dt/dy) - t = 0
dt/t = dy/y donne ln(t) = ln(y)+Constante
t = C*y
ED compète, avec "variation de la constante" :
On remplace C par f(y)
t = y f ; dt/dy = f + y (df/dy)
y (dt/dy) -t = y = y (f + y (df/dy)) - y f
y = y² (df/dy)
df/dy = 1/y
f = ln(y) +constante
t = y f = y ln(y) + C*y
Les solutions de l'équation y' = y/(y + t) sont les fonctions t(y) définies par :
t(y) = y*ln(y) + C*y , avec C = constante quelconque.
Les fonction y(t) sont les fonctions réciproques de t(y). Elle ne s'expriment pas avec un nombre fini de fonctions usuelles ( il faut faire appel à une fonction spéciale : la fonction W de Lambert).
En posant C = ln(c)
t = y ln(c y)
(c y) ln(c y) = c t
avec c y = exp(X)
X exp(X) = c t
X = W(c t)
y = (1/c) exp( W(c t) )

[alavacommejetepousse]

. J'ai pensé à la méthode z = y/t, mais ca ne mene nulpart. Alors, comment faire?

merci.

bonjour


y ' = f(y/t) équa diff à variables homogènes

z = y/t donne une équa diff à variables séparables ; ça doit mener bel et bienau résultat.

[JeanJ]

Salut,

Ben314 :
J'ai l'impression que ça marche en posant z=y/(y + t)

En effet, en principe cela peut marcher. Mais je te souhaite bien du plaisir... As-tu essayé ?

MathematicienPoche:
z = y/t donne une équa diff à variables séparables ; ça doit mener bel et bienau résultat.

En effet, en principe cela peut marcher. Mais je te souhaite bien du plaisir... As-tu essayé ?
Au lieu de z = y/t je poserais plutôt f = t/y et cela reviendrait exactement au même que la méthode indiquée dans mon post précédent.

[alavacommejetepousse]

En effet, en principe cela peut marcher. Mais je te souhaite bien du plaisir... As-tu essayé ?
.

bonjour

guère de plaisir à résoudre ça mais guère plus de 30sec pour le faire

[Ben314]

Soit
Si alors donc puis


Où est bijective sur chacun des intervales 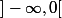, 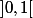et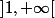
Les solutions se présentent donc sous la forme où 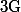désigne une des bijection réciproques de donc .
On voit en particulier ici que déterminer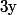 "plus précisément" revient trés exactement à déterminer 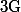"plus précisément" ce qui, il me semble, montre qu'il n'y a pas de meilleures méthode de résolution.

[JeanJ]

En effet, c'est à peu près ce à quoi j'étais arrivé en essayant ta méthode ( "à peu près" voulant dire que je n'avais pas les mêmes notations, bien évidemment)
Quant à la bijection réciproque, si on l'explicite, c'est là que la fonction W de Lambert apparaît.
On arrive aussi à la même conclusion par la méthode proposée par alavacommejetepousse.
MathematicienPoche, qui a posé le problème, n'a plus que l'embarras du choix. Tant mieux !

Remarque pour Ben314 :
il ne faut pas prendre mal l'expression "Mais je te souhaites bien du plaisir" que j'ai employée en boutade. Cela ne voulais pas dire que c'était très difficile mais seulement qu'il y avait beaucoup plus simple :
En effet, pour cette équation y' = y/(y+t) il est nettement plus simple de rechercher t(y) au lieu de y(t). En une ligne, tout est dit !
L'équation d'inconnue t(y) est t' = (y+t)/y qui est linéaire :
y t' -t =y
Et le tour est joué.

[ffpower]

Ouais, mais c'est du physicien, et donc pas trés rigoureux. Quelque part, tu suppose que y est bijective..Ce qui aprés ne semble d ailleurs pas être le cas, donc faudrait raisonner sur le fait que y est localement bijectif la ou la dérivée ne s annule pas, ou un truc du genre..Donc rendre ta demo rigoureuse semble finalement plus compliqué que les 2 autres démos..

[MathematicienPoche]

merci beaucoup! vous m'avez tous plus qu'aidé!

[grikor]

Bonjour,
si y=zt; y'=z't+z=(z+1)/z; z't=-z²/(z+1)

(z+1)/z²*dz=-dt/t (équation séparable)

[alavacommejetepousse]

Bonjour,
si y=zt; y'=z't+z=(z+1)/z; z't=-z²/(z+1)

(z+1)/z²*dz=-dt/t (équation séparable)

je dirais même plus:
équation (à variables) séparée(s).

[JeanJ]

Ouais, mais c'est du physicien, et donc pas trés rigoureux.

J'adore !
J'ai fait exprès d'utiliser la notation dy/dt au lieu de y' pour agiter le chiffon rouge. J'aurais été déçu s'il n'y avait pas eu de réaction.
Et en point de départ, écrire y'=y/(y+t) sans savoir si y(t) est bijective ou non, c'est rigoureux ?

[alavacommejetepousse]

il suffit de se placer sur un intervalle où ni t ni y s 'annulent pour résoudre proprement avec z = y /t; la longueur de l'intervalle dépendra a posteriori du choix de la constante d'intégration.

[Black Jack]

Ouais, mais c'est du physicien, et donc pas trés rigoureux. Quelque part, tu suppose que y est bijective..Ce qui aprés ne semble d ailleurs pas être le cas, donc faudrait raisonner sur le fait que y est localement bijectif la ou la dérivée ne s annule pas, ou un truc du genre..Donc rendre ta demo rigoureuse semble finalement plus compliqué que les 2 autres démos..

Ouais, mais c'est du physicien, et donc pas trés rigoureux.

Et puis quoi encore ? :happy2:
Je ne parle pas ici du raisonnement de l'un ou l'autre dans ce topic mais de la manière d'aborder les équations différentielles des Physiciens en remplaçant les dérivées par un rapport de 2 infiniments petits.

Il y a très longtemps que les physiciens font cela presque "par instinct", mais il n'est plus question de dire que cette manière de faire n'est pas rigoureuse. Un nouveau pan des mathématiques l'ANS (analyse non standard) a été développé (vers 1960) et a défini avec toute la rigueur voulue la notion d'infiniment petits... et leur emploi dans la résolution des équations différentielles.

On en parle un peu sur ce lien : http://fr.wikipedia.org/wiki/Analyse_non_standard

La manière de procéder des physiciens rejoint la théorie mathématique de l'ANS qui est tout à fait rigoureuse.

L'ANS va plus loin que ce qui est employé par les physiciens avec notamment les hypernaturels, et cela n'est pas très facile parfois à utiliser, mais c'est une autre histoire.

:zen:

[JeanJ]

Je ne parle pas ici du raisonnement de l'un ou l'autre dans ce topic mais de la manière d'aborder les équations différentielles des Physiciens en remplaçant les dérivées par un rapport de 2 infiniments petits.
Il y a très longtemps que les physiciens font cela presque "par instinct", mais il n'est plus question de dire que cette manière de faire n'est pas rigoureuse. Un nouveau pan des mathématiques l'ANS (analyse non standard) a été développé (vers 1960) et a défini avec toute la rigueur voulue la notion d'infiniment petits... et leur emploi dans la résolution des équations différentielles

Bravo Black Jack !
je ne peux qu'applaudir car je milite dans ce sens depuis longtemps.
Mon article "Une querelle des Anciens et des Modernes" reste encore de temps en temps d'actualité, mais de moins en moins souvent. Il tombera bientôt complètement dans l'oubli et c'est très souhaitable.

[ffpower]

L'ANS est faite pour "simuler" les dx en effet, mais êtes vous sur que résoudre une equa diff "a la physicienne" ( celle ci dessus par exemple ) donne forcément une preuve rigoureuse en ANS? Moi j'ai plus l'impression que l'ANS sert d'excuse aux physiciens pour dire " Eh vous voyez en fait, on était rigoureux nous!" alors qu'ils en ont pour la plupart juste entendu parler de loin..Je me demande combien de physiciens ont étudiés les regles de l ANS enfin d en comprendre la rigueur et les limites. Pour ma part j'ai essayé de lire la page wiki ya quelques temps, en temps que "matheux" si je puis dire, et j y aie pas compris grand chose. Ca a l air de ressembler plus a de la logique qu autre chose..Et doit pas y avoir beaucoup de physiciens qui s interessent a la logique ( déja que ca interesse pas tellement de matheux :) )
Mais bon, je suis quelqu un de sceptique mais pas de borné, donc on va dire que si vous refaites la preuve ci dessus rigoureusement en théorie ANS, en citant les propositions utilisées, vous me convaincrez probablement.. :zen:

[Black Jack]

ffpower,

Je pense que tu prends le problème à l'envers.

Les physiciens n'ont jamais été tracassés par la soi-disant non rigueur que les mathématiciens leur prêtaient lorsqu'ils remplaçaient une dérivée par le rapport de 2 infiniment petits.

L'ANS n'a pas été développée par des physiciens mais par des mathématiciens.
Et cette branche des mathématiques a permi de montrer que la manière de faire des physiciens n'avait rien "d'illicite".
Mais maintenant, grâce à l'ANS, on a une définition rigoureuse de la notion d'infiniments petits et la manière de faire des physiciens est passée de "l'intuition" à la rigueur.

Cela ne changera en rien la manière de travailler des physiciens,l'ANS est pour moi plus utile pour qu'enfin les mathématiciens puissent dormir tranquilles et ne puissent plus mettre en doute les résultats obtenus par les physiciens sous une fausse excuse de non rigueur.

Je ne vais certainement pas me lancer ici dans un cours sur l'ANS (ce dont je suis d'ailleurs bien incapable), mais il existe de très bons bouquins sur le sujet.
*******
Bonjour en passant à JeanJ, JJ ou JJA que je croise, sur différents forums, depuis de nombreuses années et dont j'apprécie toujours les interventions.

:zen: