Corps de fonctions d'une variable
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 02 Fév 2010, 22:07
par Doraki » 02 Fév 2010, 22:07
Bonsoir.
Soit a et b dans Q, distincts
On considère
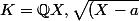(X-b)}\))
.
Il faut trouver un y dans K tel que K = Q(y).
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 02 Fév 2010, 22:57
par ffpower » 02 Fév 2010, 22:57
Au hasard..La somme?
Avec les algébriques, ca marche presque a chaque fois, mais c est peut etre plus rigide avec les transcendants..

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 02 Fév 2010, 23:01
par Ben314 » 02 Fév 2010, 23:01
Perso, je vote pour
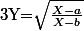
pas totalement au hasard :
Si
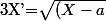(X-b)})
alors
)
Dans l'autre sens,
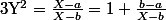
donc
)
et
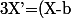Y=\frac{(b-a)Y}{Y^2-1}\in{\bb Q}(Y))
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 02 Fév 2010, 23:08
par Doraki » 02 Fév 2010, 23:08
ffpower, en effet avec des trucs transcendants ça marche plus du tout, et il y a des extensions transcendantes qui n'ont pas d'éléments primitifs.
Si on met un polynôme de degré 3 sous la racine ça devient impossible d'écrire K comme un Q(y).
Et ben314, tu as la bonne variable, et c'est pas au hasard vu que y'en a pas des masses qui conviennent.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités