Opérateurs.......

[houda 20]

Bonsoir
voilà, j'ai besoin de trouver deux opérateurs A1 et A2 positifs tel que

A1+A2=A et A1*A2=A2*A1=0
avec A un opérateur auto adjoint quelconque
on pourra chercher les opérateurs en fct de A*A car ce dernier est tjrs positif
c'est ça ce que j'essaye de faire, de relier A*A avec l'opérateur A de façon à obtenir A1 et A2

merci à vous

[alavacommejetepousse]

bonsoir

si A1 et A2 existent ils commutent avec A

dans le cas où A admet un sous espace propre E(s) associé à une valeur propre s strictement négative de dimension 1 , X un vecteur propre associé

AX = sX donne A1AX = sA1X = AA1X donc A1X est dans E(s) donc colinéaire à X d'où A1X = s'X , s' étant positif puisque A1 l'est de même, pour A2, A2X = s" X et s' + s " = s n'est pas positif.
conclusion A1 et A2 ne peuvent exister dans ce cas.

[houda 20]

bonsoir
merci pour la réponse

si A1 et A2 existent ils commutent avec A
je ne vois pas d'ou tu as conclut ça?

dans le cas où A admet un sous espace propre E(s) associé à une valeur propre s strictement négative de dimension 1 , X un vecteur propre associé

AX = sX donne A1AX = sA1X = AA1X donc A1X est dans E(s) donc colinéaire à X d'où A1X = s'X , s' étant positif puisque A1 l'est de même, pour A2, A2X = s" X et s' + s " = s n'est pas positif.
conclusion A1 et A2 ne peuvent exister dans ce cas.

pour ça je ne comprends vraiment pas très bien!!
on commence juste à nous introduire les notions des valeurs propres et le spectre et .....
mais ce que je peux affirmer qu'ils existent car c'est un exo de td et le prof a assuré leurs existences......

bon, malgré ça je ne sais pas,.........

[Ben314]

Bonsoir,
Tout d'abord, le fait que A commute avec A1 et A2 est "bète comme choux" :
A.A1=(A1+A2).A1=A1.A1 car A2.A1=0
A1.A=A1.(A1+A2)=A1.A1 car A1.A2=0
Idem pour A2

Ensuite, pour la question de départ, dans quel contexte est tu ?
Espaces réels ou complexes ?
dim finie ou pas ?
le terme d'opérateur positif veut-il dire symétrique ou hermitien positif ? (i.e.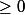 pour tout X)

Est tu sûr que ton énoncé est juste et que ce ne serait pas plutôt A=A1-A2 ?

[houda 20]

Bonsoir
normalement c'est des opérateurs sur un C hilbert
opérateur positif veut dire hermitien positif
pour l'énoncé, c'est A1+A2 et non pas -

[Ben314]

Si c'est un +, il y a quelque chose qui m'échape...
Il me semble bien que la somme de deux opérateurs positifs est un opérateur positif, donc je vois pas comment on pourrait écrire les opérateurs non positifs comme une somme d'opérateurs positifs.

[alavacommejetepousse]

alors si en plus d'être positisf ils doivent être autoadjoints alors commutant tous trois ils seront simultanément orthodiagonalisables et la somme de A1 et A2 a fortement intérèt à être positive également

[Ben314]

Bon, malgrés ce que tu dit, je pense qu'il faut montrer que A=A1-A2.

Si tu as déjà vu que tout opérateur autoadjoint positif admet une unique racine carrée, alors considére B=A1+A2 et montre que B est la racine carrée de A². Tu en déduira qui sont A1 et A2...

[alavacommejetepousse]

si on ne veut que l existence de A1 et A2 avec A = A1-A2

on prend une base de diagonalisation de A

les r premiers vecteur associés à des valeurs propres positives les dernièrs à des négatives strictes

on prend A1 qui coincide avec A sur les premiers et vaut à sur les derniers

et A2 qui vaut sur les premiers et coincide avec -A sur les derniers.

[houda 20]

oui, tu as parfaitement raison Ben
je n'ai vraiment pas fait attention à ça

[houda 20]

merci alavacommejetepousse mais j'ai besoin de les retrouver

[Ben314]

Aprés, là où je me rapelle plus (le seul cours sur les C*-algèbres que j'ai suivi, ça date un peu...) c'est si les arguments de alavacommejetepousse sont valables sur un hilbert pas forcément de dim finie, ni même séparable...
Je sais plus du tout s'il existe une notion de "base de diagonalisation" dans le cas non séparable...

Si j'y pense, je demanderais.

[houda 20]

Ben tu veux dire on met
A=A1-A2
B=A1+A2

ON TROUVERA

A1=(B+A)/2 A2=(-B+A)/2

mais ces deux là , ne sont pas nécéssairement positifs, non

bien qu'ils vérifient tout le reste.........