Sous espace. base.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
theloulou
- Membre Naturel
- Messages: 65
- Enregistré le: 15 Jan 2009, 20:02
-
 par theloulou » 31 Jan 2010, 19:17
par theloulou » 31 Jan 2010, 19:17
Bonjour, je dois trouver une base du sous espace F de R4. Sachant que F est défini par les équations x+y+z+t=0 et x+2y+3z+4t=0. quelle éthode dois je utiliser? Merci d'avance.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 31 Jan 2010, 19:18
par Nightmare » 31 Jan 2010, 19:18
Salut,
As-tu vu la notion de dimension?
-
theloulou
- Membre Naturel
- Messages: 65
- Enregistré le: 15 Jan 2009, 20:02
-
 par theloulou » 31 Jan 2010, 20:07
par theloulou » 31 Jan 2010, 20:07
oui dans mon cours d'hier mais je n'ai pas du tout compris ce point. l'explication n'était pas claire. c'est pourquoi une méthode ou un automatisme pourrait m'avancer
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 31 Jan 2010, 20:45
par Finrod » 31 Jan 2010, 20:45
Le but des exos est de comprendre, en toute logique, pas de trouver des méthodes pour les faire sans avoir compris.
En toute généralité, il te faut trouver une famille libre et génératrice mais l'exercice est beaucoup plus simple en connaissant la notion de dimension et le thm du rang.
tu connais le thm du rang ?
-
theloulou
- Membre Naturel
- Messages: 65
- Enregistré le: 15 Jan 2009, 20:02
-
 par theloulou » 31 Jan 2010, 20:58
par theloulou » 31 Jan 2010, 20:58
non justement on nous a dit que l'on pouvait aller plus vite avec la méthode que l'on verra au prochain cours, ais pour l'instant on doit passer par une autre voie que le théorème du rang
-
Near
- Membre Relatif
- Messages: 312
- Enregistré le: 10 Déc 2008, 16:42
-
 par Near » 31 Jan 2010, 21:17
par Near » 31 Jan 2010, 21:17
salut :we:
est-ce que cette méthode marche...
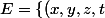\in \mathbb{R}^4;x+y+z+t=x+2y+3z+4t=0 \right \}.)
posons
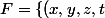\in \mathbb{R}^4;x+y+z+t=0 \right \}.)
on a

et

donc

et

.
par suite dimension de
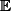
peut être 2 ou 1...je peux rien dire

-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 31 Jan 2010, 22:19
par Nightmare » 31 Jan 2010, 22:19
Une méthode élémentaire consiste à écrire que le système se ramène à

Ainsi si u=(x,y,z,t) est dans E, on peut écrire à la vue de ces équations que
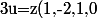+t(1,-3,0,1))
.
On vient d'exhiber deux vecteurs générateurs, qui ont le bon goût d'être non colinéaires. La famille formée des deux est donc une base de E.
-
theloulou
- Membre Naturel
- Messages: 65
- Enregistré le: 15 Jan 2009, 20:02
-
 par theloulou » 31 Jan 2010, 23:19
par theloulou » 31 Jan 2010, 23:19
je comprend pour la méthode élémentaire et le but recherché mais pas pour u= z(...)+t(...) coment on procède sur cette étape?
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 31 Jan 2010, 23:32
par Finrod » 31 Jan 2010, 23:32
x,y,z,t sont les coordonnées de ton vecteur , i.e. du vecteur u= (x,y,z,t) dans l'esp vect
Si x = z+2t , tu développes u= (z,y,z,t) +(2t,y,z,t) et ainsi de suite, tu trouveras le même résultat.
-
theloulou
- Membre Naturel
- Messages: 65
- Enregistré le: 15 Jan 2009, 20:02
-
 par theloulou » 31 Jan 2010, 23:44
par theloulou » 31 Jan 2010, 23:44
je dois faire une erreur je trouve u= z(1,-2,1,0) + t(2,-3,0,1)..?
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 31 Jan 2010, 23:48
par Finrod » 31 Jan 2010, 23:48
theloulou a écrit:je dois faire une erreur je trouve u= z(1,-2,1,0) + t(2,-3,0,1)..?
non c'est Nightmare qui a oublié un "2". C'est bon.
-
theloulou
- Membre Naturel
- Messages: 65
- Enregistré le: 15 Jan 2009, 20:02
-
 par theloulou » 31 Jan 2010, 23:50
par theloulou » 31 Jan 2010, 23:50
ah très bien, merci pour votre aide. donc j'ai trouvé une famille génératrice avec ces 2 vecteurs. Et je dois montrer que cette famille est libre et ça suffit pour ma base?
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 31 Jan 2010, 23:53
par Finrod » 31 Jan 2010, 23:53
C'est la définition d'une base : libre et génératrice.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
