Dm pour demain .

[liloudu82]

Bonjour à tous , j'aurai besoin d'aide pour cet exercice s'il vous plait.

Voici l'énnoncé :

Soit la parabole (C) d'équation y= 2x² + bx + 3 et la droite (d) d'équation y= x+1 .

1) Pour quelle(s) valeurs de b , (C) et (d) ont-elles un seul point en commun?
2) Pour quelle(s) valeurs de b , (C) et (d) n'ont-elles aucun point en commun?

D'avance merci ,

Bisous .

[Dinozzo13]

Pour le 1er :
(C) et (d) ont un point en commun si et seulement si :

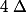
et si une fois que tu as réduit l'équation le discriminant est nul.
Je te laisse deviner pour le 2e.

[liloudu82]

est ce que tu peux m'aider à détailer le calcule s'il te plait ?

[liloudu82]

Je trouve : 2b² + 2b - 16

:/ J'y arrive pas !

[Dinozzo13]

Hé bien, tu dis que les abscisses des points d'intersections de (C) et (d) sont solutions de l'équation :


Tu appliques le discriminant :
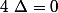
Puis tu résous pour trouver .
Si alors (C) et (d) ont un seul point en commun

[liloudu82]

D'accord :) Merci beaucoup . Et le deuxième je fais comment s'il te plait ! :id:

[liloudu82]

tu es toujours là .?

[Sylviel]

Et bien il n'y a pas d'intersection s'il n'y a pas de racines à la différence. La différence est un trinome (celui calculé précédémment), dans quel cas n'as-t-il pas de solutions ?