Bonsoir,
j'ai un problème sur la résolution de cette intégral :
borne inférieure : 1
borne supérieure : a
intégrale(2/(e^(x)+1) dx
est ce égale à : 2* intégrale (1/(e^(x)+1)
= 2* [1/e^x]ln(e^(x)+1)]
= (1/e^(a))*ln(e^(a)+1) - (1/e)*ln(e+1)
Si ce n'est pas ca comment dois je m'y prendre svp ?
Intégral
11 messages
- Page 1 sur 1
C'est un bon début, mais là :
Ca ne va pas du tout : tu doit exprimer dx en fonction de u et de du pour que dans ton intégrale aprés changement de variable, tous les x sans exception ait disparus et que la seule variable soit u (c'est pas pour rien que l'on apelle ça un changement de variable)Nicodu69 a écrit:dx = 1/e^(x) du
...2*(intégrale(1/u * 1/e^(x))) du
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
C'est pourtant simple : tu fait un changement de variable, c'est comme si on te demande de convertir en poid le volume de 1425 Litres d'eau et que tu répond que cela fait 1000Kilo et 425 Litres : c'est un résultat totalement inutilisable car ce n'est ni un poid, ni un volume !!!!!
Ici, c'est pareil : tu ne doit avoir QUE DES 'x' ou bien QUE DES 'u', un résultat 'intermédiaire' est totalement inutilisable.
DONC ton "dx=1/e^x du" ne va pas (à droite, il y a des litres ET des kilos)
il faut un "dx=fonction_de_u du".
Deux méthodes :
1) Soit tu part de ton "dx=1/e^x du" et tu écrit e^x en fonction de u
2) Soit tu commence par chercher x en fonction de u puis (en dérivant) tu en déduit dx en fonction de u et de du.
Ici, c'est pareil : tu ne doit avoir QUE DES 'x' ou bien QUE DES 'u', un résultat 'intermédiaire' est totalement inutilisable.
DONC ton "dx=1/e^x du" ne va pas (à droite, il y a des litres ET des kilos)
il faut un "dx=fonction_de_u du".
Deux méthodes :
1) Soit tu part de ton "dx=1/e^x du" et tu écrit e^x en fonction de u
2) Soit tu commence par chercher x en fonction de u puis (en dérivant) tu en déduit dx en fonction de u et de du.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
C'est quasi bon (sauf un 'x' qui devrait être un 'a' qui est surement une faute de frappe : une fois qu'on a intégré en x, eh ben des 'x' forcément, y'en a plus...)
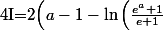 \right))
Pour résoudre ton indetermination, commence par couper le log en deux : log(A/B)=... car il y a une partie que ne sert à rien.
Ensuite, dans le , c'est clairement le
, c'est clairement le  le plus important => met le en facteur et sort le du log : log(A*B)=...
le plus important => met le en facteur et sort le du log : log(A*B)=...
Ton indétermination va disparaitre...
Pour résoudre ton indetermination, commence par couper le log en deux : log(A/B)=... car il y a une partie que ne sert à rien.
Ensuite, dans le
Ton indétermination va disparaitre...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
