Equadiff

[Shym]

Lors de mon dernier partiel il est tombé

y''-y'=x+sinxcosx

donc je resout l'equation m²-m=0

j'obtient y= Aexp(0x)+Bexp(1x)

ensuite
et bien je bloque un peu... je pensais décomposé en deux termes

le premier résoudre avec =x j'aurais Y0=x(A1+B1x)

et ensuite avec sinxcosx

mais dans mon cour je ne vois pas du tout sous quelle forme mettre mon Y0 pour sinxcosx.

si quelqu'un peut m'aider !!!
merci beaucoup

[Ben314]

Salut,
Peut être en écrivant sin(x)cos(x)=sin(2x)/2...

[ferfelue]

quand on veut résoudre une équation du 2 ordre on trouve d'abords la solution de l'équation homogène ce que ta trouver y=A+ B exp(1)
puis on cherche la solution particulier de (e) notre équation non homogène cela en utilisant la méthode de la variation de la variable tu prend p(t)=k(t)y(t)

[Shym]

ok merci j'oublie toujours la linéarisation

mais ici dans mon problème j'ai deux solution particulière,

la première y=x(A+Bx)
et la seconde y=Pn (x) cos(;)x) + Qn(x) sin(;)x)

je fais quoi je les additionnes dessuite? ou bien je traite jusqu'à la fin et j'additionne qu'au niveau du résultat

[Ben314]

En général, il est beaucoup plus simple de chercher indépendament les deux soluces particulières et de ne les ajouter qu'à la fin.

[busard_des_roseaux]

pourquoi une équation du second degré en m alors que
l'équa diff est du 1er ordre ? (z=y')

[Shym]

Bien joué je ne l'avais pas vu
:we:

[SlowBrain]

Euh... Pardon... quelques petits détails si je puis me permettre... j'espère que tu n'as pas gardé ton exp(0x) pendant tous tes calculs?? :) Ensuite la méthode de la variation de la constante marche bien au premier degré (comme ici à une vache près), mais j'ai des doutes mais au degré supérieur, vous êtes sûr que ça marche aussi bien?? (sur mes gribouillis ça ne donne pas des choses assez potables donc j'aimerais bien votre avis)

[Ben314]

La méthode de variation de la constante marche quelque soit le degrés MAIS... il faut regarder l'équa.diff linéaire comme du étant du premier degrés en considérant le vecteur si l'équation est de degrés .
Par exemple pour une équa.diff. de degrés 2, si une base des solutions de l'équa.diff. homogène associée est alors la méthode de variation de la constante consiste à injecter dans l'équa.diff. avec second membre une fonction f telle que :
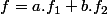(où et sont des fonctions)
mais aussi telle que
(ce qui signifie que )
Si tu "oublie" la deuxième relation, tu ne risque pas de trouver les solutions (2 inconnues et et une seule équation....)

P.S. Quand elle aboutit (et c'est le cas ici), il faut toujours priviligier la méthode "par tatonement" c'est à dire consistant à écrire "essayons comme par hazard ce type là de fonction..."
C'est parfaitement authorisé vu qu'on ne cherche qu'une seule solution et pas toutes, et si on y arrive (à "essayer" la bonne fonction) ça va beaucoup plus vite.