Fonction affine - solutions de f(x)=0

[Starky]

Bonsoir, j'aurais besoin d'une petite aide pour un exo. Le but de celui-ci est d'étudier dans un premier temps de le sens de variation de la fonction

f(x)=2x³-3x²-1

Je trouve donc la dérivée de cette fonction,

f'(x)=6x²-6x

Je trouve que la f'(x)=0 pour x=0 ou x=1
d'où le tableau de variation (désolé, c'est un peu artisanal >_<)

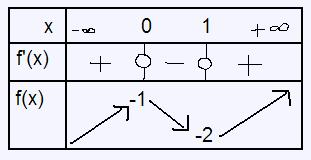
Ensuite, il faut en déduire que f(x)=0 n'admet qu'une solution sur ]1;2[

Il faut donc dire que f(x), est strictement croissante sur ]1;+i[ donc sur ]1;2[
et que f(1) et f(2) sont de signes contraires.

J'en arrive enfin à ma question, comment prouver que f(x)=0 n'admet q'une solution sur |R ?

[Ericovitchi]

Oui tout ça a l'air tout à fait juste.

f(x)=0 n'admet qu'une seule solution parce que l'étude des variations montre que la fonction ne coupe l'axe des x qu'une seule fois pardi.

[Starky]

Oui mais il ne faut pas le démontrer ?

[massengo]

C'est facile, f est croissante et continue sur l'intervalle [1;2] alors f est bijective sur cet intervalle. cela veut dire que a chaque antécédent y correspond un x unique tel que f(x)=y. donc pour 0 il n'existe qu'un seul point x tel que f(x)=0. f(1)= -2 et f(2)=3, comme f croit de -2 a 3 et est continue alors passe bien par le point 0. Donc il existe un x dans [1;2] tel que f(x)=0. C'est le théorème des valeurs intermédiaires.