Pédagogie: logarithme népérien

[mathelot]

re,

j'ai lu un papier qui m'a bien plû dernièrement: un universitaire soulignait que John Néper avait inventé les logarithmes (décimaux) bien avant que Newton (versus Leibniz) n'inventent les fonctions dérivées et le calcul intégral.

Comme conséquence, on devrait pouvoir expliquer, dès la quatrième française, et très certainement en classe de Seconde , les logarithmes.

Il suffit d'avoir une première droite graduée sur laquelle varient les "exposants"
n,m,n+m et une seconde droite graduée sur laquelle varient leurs puissances


Après, on prolonge en une fonction la fonction de N dans N :
par un argument de cinématique (des points mobiles se correspondent sur les deux droites).


Quelqu'un a des infos plus précises sur ce logarithme "préhistorique" ?

merci d'avance.

[Ben314]

Salut Mathelot,
Moi qui suis un vieux con, ça me fait un tout petit peu penser aux règles à calculer de nos ancètres (préhistoriques). Je sais pas en quelle classe les élèves apprenaient à ce servir de cet outil (je suis pas SI vieux que ça... :zen: ) mais ça aurait peut-être pu être effectivement au collège...

En ce qui me concerne, l'explication "cinématique" du prolongement de N à R, je préfère un argument du type "on voudrait que la formule 10^(a+b)=10^a*10^b reste vrai, ce qui conduit à 10^(3,5)=10^3*10^0,5
et à 10^0,5 =le nombre dont le carré vaut 10^1 (i.e. la racine de 10)
puis à 10^0,25=racine(10^0,5)...

[SlowBrain]

Effectivement, c'est exactement le principe de la règle à calculer! Je ne sais pas où j'ai rangé la mienne, mais je m'en servais pour effectivement illustrer les propriétés algébriques du log. Cependant enseigner le log à des secondes alors que les premières, y compris scientifiques, se gourent assez souvent sur les simplifications de fractions.....

[Ben314]

...enseigner le log à des secondes alors que les premières, y compris scientifiques, se gourent assez souvent sur les simplifications de fractions.....

C'est pas faux...

[Finrod]

C'est pas faux...

Sort de ce corps, Perceval !

[Ben314]

Sort de ce corps, Perceval !

C'est ma série "culte" :
Angarade : Lorsque je me regarde dans un mirroir, je me sens insipide...
Perceval : C'est pas faux...

Plus tard à table avec le roi :
Le roi : "Y'a pas à dire, les saucisse, c'est fameux"
Perceval : "Oui, mais ça ne vaut pas les cotelettes"
Le roi : "C'est pas faux"
Perceval : "Vous savez pas ce que c'est des cotelettes ?"

[mathelot]

Effectivement, c'est exactement le principe de la règle à calculer! Je ne sais pas où j'ai rangé la mienne, mais je m'en servais pour effectivement illustrer les propriétés algébriques du log. Cependant enseigner le log à des secondes alors que les premières, y compris scientifiques, se gourent assez souvent sur les simplifications de fractions.....

bah vi, il y a du log mais il n'y a pas:
- fonctions dérivées
- calcul intégral, primitive, signe "somme" etc...

puisque ça n'existait pas du temps de John Neper.

Il faudrait arrêter d'écrire que ce sont les élèves qui sont faibles.
ce sont plutôt les gens qui fabriquent les programmes... exemples:

- ils n'enseignent plus les mesures algébriques pour le théorème
de Thalès

pourtant cette notion supprime les cas particuliers
- ils apprennent aux enfants à résoudre les systèmes linéaires par substitution (mauvaise méthode) au lieu des combinaisons linéaires
ou pivot (bonne méthode)
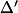
- ils n'enseignent plus le discriminant réduit du trinome
- au collège, ils n'enseignent pas la configuration orthocentrique
mais juste l'orthocentre. On ne voit bien les relations entre A,B,C,H
chaque point étant l'orthocentre des trois autres
- les racines carrées ne sont pas introduites de façon naturelle
par la courbe de la parabole ou la suite de Héron (on transforme progressivement une suite de rectangles en carrés). Ils font une
introduction des racines carrées formelle qui ne parlent pas aux élèves
- ils n'expliquent pas les fonctions monotones, par les taux d'accroissement.
le taux d'accroissement étant pourtant un bon outil qui évite les démonstrations interminables
- au collège, ils n'expliquent pas toujours que les rectangles
sont des parallèlogrammes et que les carrés sont des rectangles
- en trigo, ils n'expliquent pas toujours
que le cosinus de l'angle A est le sinus du complémentaire,
ce qui ne coûte rien
- en 1ère, ils n'expliquent pas toujours comme déterminer les coefficients
barycentriques visuellement...
- hors la filière scientifique, il y a des profs qui massacrent le calcul différentiel: j'ai vû des élèves en STG ou STI, je ne sais plus,
qui ont commencé les fonctions dérivées par un formulaire
de dérivées classiques.


etc,etc..

[SlowBrain]

Et ce n'est pas uniquement le programme qui est mauvais. Tous les lycées n'ont pas la chance d'avoir des profs qui maîtrisent ce qu'ils enseignent (parfois tous les lycées n'ont pas la chance d'avoir des profs tout court... hum... et ce n'est pas une blague, j'ai vu des classes de seconde commencer le programme de math en février) Je suis aussi d'accord pour dire que ce ne sont pas les élèves qui sont mauvais (quand la quasi totalité d'une classe de 30 fait la même faute je vois bien que le problème n'est pas qu'ils sont bête)