Dominance stochastique

par **clicli** » 24 Jan 2010, 16:02

Bonjour,

On définit la dominance stochastique entre deux variables aléatoires par:

ssi:

Est ce que quelqu'un pourrait me dire comment je traduis ça en horizon fini, avec

?

J'ai l'impression qu'il me suffit d'avoir

mais je n'arrive pas à m'en convaincre vraiment, encore moins à le démontrer!

Merci

par **Finrod** » 24 Jan 2010, 16:23

Je dirais que les intégrales deviennent des sommes.

par **clicli** » 24 Jan 2010, 16:42

Bon je viens d'écrire le calcul pour un univers

et ma conjecture est bonne!

En fait, c'est ce t qui est trompeur dans la définition avec les intégrale, parce q'il ne correspond pas au temps qui passe!

par **clicli** » 24 Jan 2010, 16:48

Euh non, je me reprends... Ma conjecture n'est bonne que pour

Du coup, il faut s'intéresser à l'image des variables aléatoires par des fonctions convexes décroissantes...

par **Finrod** » 24 Jan 2010, 17:04

Il me semble que les intégrales que tu as données sont bien égales aux espérances.

Où trouves tu un problème ? il faut juste inverser les deux intégrales.

par **clicli** » 24 Jan 2010, 17:19

Mes intégrales ne sont égales à l'espérance que pour

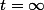
dans le cas général ou pour t suffisamment grand dans mes hypothèses.

Sinon, ça n'est pas l'espérance, et comme l'inégalité doit être vérifiée pour tout t, on arrive à

pour toute fonction W convexe et décroissante.

par **Finrod** » 24 Jan 2010, 18:11

En effet, si tu inverses

je suppose que tu as

.

J'arrive à

où f est la densité.

Soit

Dominance stochastique

Dominance stochastique

Qui est en ligne