Equation difficile

par **dame** » 23 Jan 2010, 18:43

Resoudre l'equation suivante:
5-x²=racine de (5-x)

par **Ben314** » 23 Jan 2010, 18:49

Salut,
Peut être faudrait-il songer à poser u=racine(5-x)... (et aussi à écrire moins gros)

par **Finrod** » 23 Jan 2010, 18:54

Tiens je trouve pas de solution.

Déjà, tu as X<5 tu élève au carré

, on vérifie qu'elle n'a pas de solution du tout en faisant u tableau de signe.

par **dame** » 23 Jan 2010, 19:05

Finrod a écrit:Tiens je trouve pas de solution.

Déjà, tu as X<5 tu élève au carré

, on vérifie qu'elle n'a pas de solution du tout en faisant u tableau de signe.

monsieur, le coefficient de x² est -10

par **Finrod** » 23 Jan 2010, 19:09

En effet. Le résultat reste inchangé.

par **JeanJ** » 23 Jan 2010, 19:12

Salut,
Finrod -> Attention, ce n'est pas -5 x² , c'est -10 x²
dame -> L'équation indiquée par Finrod (après correction) a 4 racines réelles. mais seulement deux satisfont à l'équation initiale (avec V signifiant racine carrée ) :
(1-V(17))/2
(-1+V(21))/2
Petite question : dans ton énoncé, est-ce que c'est 5-x² comme tu l'as écrit ?
Ce n'est pas (5-x)² par hasard ?

par **Finrod** » 23 Jan 2010, 19:26

En effet, je croyais que la situation se simplifiait mais en fait non.

Il y a 4 solutions mais j'ai l'impression que les 4 se retrouvent inferieure à 5 et donc acceptable...

Après, à part par maple ou autre, pour les calculer..

edit : bon non ok, il n'y a que deux solutions.

par **dame** » 23 Jan 2010, 19:26

JeanJ a écrit:Salut,
Finrod -> Attention, ce n'est pas -5 x² , c'est -10 x²
dame -> L'équation indiquée par Finrod (après correction) a 4 racines réelles. mais seulement deux satisfont à l'équation initiale (avec V signifiant racine carrée ) :
(1-V(17))/2
(-1+V(21))/2
Petite question : dans ton énoncé, est-ce que c'est 5-x² comme tu l'as écrit ?
Ce n'est pas (5-x)² par hasard ?

non, j'écris 5-x²

par **Finrod** » 23 Jan 2010, 19:54

J'ai touvé une méthode non bourrin !!!!!!!!!!!!!!

Les courbe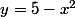

et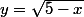

s'obtiennent par symétrie par rapport à la droite d'équation y=x.

(sauf que dans la racine, un des côté de l'hyperbole n'apparait plus.

Donc ça donne une des deux solutions, qui doit se trouver sur la première bissectrice, i.e. est solution de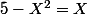

(c'est la solution en

de jean.

Pour la deuxième solution, il faut changer X en -X et il y a une méthode similaire. A la discrétion du lecteur.

par **dame** » 23 Jan 2010, 20:52

Finrod a écrit:J'ai touvé une méthode non bourrin !!!!!!!!!!!!!!

Les courbe et s'obtiennent par symétrie par rapport à la droite d'équation y=x.

(sauf que dans la racine, un des côté de l'hyperbole n'apparait plus.

Donc ça donne une des deux solutions, qui doit se trouver sur la première bissectrice, i.e. est solution de

(c'est la solution en de jean.

Pour la deuxième solution, il faut changer X en -X et il y a une méthode similaire. A la discrétion du lecteur.

comment on touve la deuxième solution à partir de cette méthode???

par **Finrod** » 23 Jan 2010, 21:05

C'est un peu plus complexe, je l'écrit bien et je rajoute en édit.

tu fait la symétrie par rapport à Y=X.

Sur ton dessin, le second point d'intersection devient alors le premier. ça se justifie en regardant les images des courbes.

Le symétrique de l'équation donne lui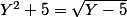

puis la c'est ok, tu fais la même méthode. le point est aussi sur la droite Y=X

par **Finrod** » 23 Jan 2010, 21:14

Putain d'exo quand même

maintenant ma pizza est cramée et j'ai faim.

par **Doraki** » 23 Jan 2010, 21:35

x4 - 10x² + x + 20 = (x²+x-5)(x²-x-4)

Le x²+x-5 correspond bien aux deux points fixes de x -> 5-x².
Mais comment tu peux retrouver géométriquement les deux autres solutions ?
(elles sont sur la droite y = -x+1)

par **Finrod** » 23 Jan 2010, 21:40

En prenant le symétrique par rapport à Y=X on change l'équation.

Le second point d'intersection est le point fixe de x²+5=x cette fois.

ça correspond à l'intersection du symmétrique de l'hyperbole par rapport à "y=0" et de la racine. (Si on fait un dessin).

par **Doraki** » 23 Jan 2010, 21:58

Nan je comprends pas comment tu peux trouver géométriquement des informations sur le point d'intersection qui est dans le quadrant x < 0 et y > 0.

(en faisant une symétrie par rapport à X=Y on ne change rien au dessin vu qu'il est déjà symétrique, je vois pas où tu veux en venir)

(le dessin c'est bien y = 5-x² et x = 5-y² ?)

par **Finrod** » 23 Jan 2010, 22:25

oui, tu as raison, il n'y a pas assez d'axes de symétrie, avec la méthode que j'ai donné juste au dessus, on trouve une deuxième fois le même point.

donc il faut finir par le calcul en effet.

Equation difficile

equation difficile

Qui est en ligne