Réccurence F(n) de la dérivée de f(x)=xe^(-2x)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
jhondoe
- Membre Naturel
- Messages: 25
- Enregistré le: 26 Nov 2009, 18:55
-
 par jhondoe » 21 Jan 2010, 20:46
par jhondoe » 21 Jan 2010, 20:46
Bonsoir !
Voila mon problème !
j'ai F(x)= xe^(-2x)
je dois montrer par réccurence que pour entier n et tout reel x :
F^(n)(x)= ((-2)^n + n(-2)^n-1)e^(-2x)
avec F^(1)(x)=F'(x)
J'arrive à le montrer au rang 0 avec =f(x) mais une fois que je passe au rang je trouve deux fois ((-2)^n + n(-2)^n-1) dans mon résultat est ce normal ?
et dois je trouver ca à la fin : ((-2)^n+1 + (n+1)(-2)^n)e^(-2x) ?
Merci :)

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 21 Jan 2010, 20:49
par Ben314 » 21 Jan 2010, 20:49
Salut,
Déjà, il me semble qu'il manque cruellement un "x" dans le facteur avant l'exponentielle...
Par exemple, tu devrait trouver F'(x)=(1-2x)exp(-2x)
Ensuite, la récurrence semble assez simple...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 21 Jan 2010, 20:51
par Finrod » 21 Jan 2010, 20:51
La dérivé de
e^{-2x})
est
-2f(x))e^{-2x})
.
Tu as du oublier un terme dans ton calcul parceque vu comme ça, ça marche.
-
jhondoe
- Membre Naturel
- Messages: 25
- Enregistré le: 26 Nov 2009, 18:55
-
 par jhondoe » 21 Jan 2010, 20:55
par jhondoe » 21 Jan 2010, 20:55
oui j'ai en effet oublier un x ((-2)^nx + n(-2)^n-1)e^-2x
mais je ne comprend toujours pas comment arriver à prouver que c'est vrai au rang n+1 car j'ai n donc j'ai derrivé pour donc trouver f'(n+1) et je trouve dans mon calcul :
f'(n+1) = e^-2x((-2)^n+1 x + (n+1)(-2)^n-1) - 2(-2)^n x + n(-2)^n-1)

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 21 Jan 2010, 21:02
par Ben314 » 21 Jan 2010, 21:02
Peut être faudrait-il un peu regrouper les puissances de -2 en utilisant par exemple le fait que (-2)^n=-2.(-2)^(n-1)...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 21 Jan 2010, 21:03
par Finrod » 21 Jan 2010, 21:03
Bizarre ta formule.
qu'est ce que tu appliques pour arriver là ? c'est peut être la méthode qui ne va pas ...
edit : ça ressemble à

la formule... en factorisant comme le suggère Ben donc tu es sans doute parti en

en pensant partir de
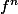
...
-
jhondoe
- Membre Naturel
- Messages: 25
- Enregistré le: 26 Nov 2009, 18:55
-
 par jhondoe » 21 Jan 2010, 21:08
par jhondoe » 21 Jan 2010, 21:08
je remplace n par n+1 nan ? :S
-
jhondoe
- Membre Naturel
- Messages: 25
- Enregistré le: 26 Nov 2009, 18:55
-
 par jhondoe » 21 Jan 2010, 21:12
par jhondoe » 21 Jan 2010, 21:12
quand je dérive j'utilise u'v+v'u
avec u'= (-2)^n+1 x + (n+1)(-2)^n)
v'= -2e^(-2x)
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 21 Jan 2010, 21:16
par Finrod » 21 Jan 2010, 21:16
Non il faut que tu le montres pour n+1 et pour cela, par hypothèse de récurrence, tu prends la formule vrai, celle pour n et tu la dérives.
-
jhondoe
- Membre Naturel
- Messages: 25
- Enregistré le: 26 Nov 2009, 18:55
-
 par jhondoe » 21 Jan 2010, 21:21
par jhondoe » 21 Jan 2010, 21:21
je dérive donc celle la ((-2)^nx + n(-2)^n-1)e^-2x) ?
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 21 Jan 2010, 21:26
par Finrod » 21 Jan 2010, 21:26
voilà.
et là, la dérivé donne la formule pour

.
-
jhondoe
- Membre Naturel
- Messages: 25
- Enregistré le: 26 Nov 2009, 18:55
-
 par jhondoe » 21 Jan 2010, 21:39
par jhondoe » 21 Jan 2010, 21:39
je suis vraiment bloqué j'dois surement mal m'y prendre...
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 21 Jan 2010, 21:46
par Finrod » 21 Jan 2010, 21:46
Dans ton premier calcul, tu as pris

et tu as dérivé, me semble-t-il.
Ton calcul était parfaitement juste, il suffisait de factoriser pour trouver

avec les indices de Ben.
Il faut que tu refasses pareil pour
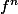
, le dériver et trouver

As-tu un pb de calcul ou est-ce la récurrence que tu ne comprends pas ?
-
jhondoe
- Membre Naturel
- Messages: 25
- Enregistré le: 26 Nov 2009, 18:55
-
 par jhondoe » 21 Jan 2010, 21:48
par jhondoe » 21 Jan 2010, 21:48
c'est un problème de calcul je pense ou de méthode
je sais que c'est un détail l'érreur mais je n'arrive pas à la trouver !!
-
jhondoe
- Membre Naturel
- Messages: 25
- Enregistré le: 26 Nov 2009, 18:55
-
 par jhondoe » 21 Jan 2010, 22:21
par jhondoe » 21 Jan 2010, 22:21
merci quand meme :)
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 21 Jan 2010, 22:26
par Finrod » 21 Jan 2010, 22:26
la dérivé de ((-2)^nx + n(-2)^n-1)e^-2x
est -2[((-2)^nx + n(-2)^n-1)e^-2x ] + e^-2x * ((-2^{n}))
qui donne pour le coef devant le x : (-2)^{n+1} et pour l'autre coeff (n+1)(-2)^{n}
bon ben ça c'est bien f^{n+1} dpnc la transmission de la récurrence fonctionne.
-
jhondoe
- Membre Naturel
- Messages: 25
- Enregistré le: 26 Nov 2009, 18:55
-
 par jhondoe » 21 Jan 2010, 22:34
par jhondoe » 21 Jan 2010, 22:34
j'comprend pa storp l'origine du -2 mis en facteur et le fait qu'il reste ceci
e^-2x * ((-2^{n}
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 21 Jan 2010, 22:37
par Finrod » 21 Jan 2010, 22:37
J'applique la formule.
Finrod a écrit:La dérivé de
e^{-2x})
est
-2f(x))e^{-2x})
.
f(x) = (-2)^nx + n(-2)^n-1)
f'(x) = (-2)^n
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
 et tu as dérivé, me semble-t-il.
et tu as dérivé, me semble-t-il. avec les indices de Ben.
avec les indices de Ben. 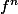 , le dériver et trouver
, le dériver et trouver 
