Série de fonctions

[nico742]

Salut, j'ai un problème pour terminer l'exo que voici :
On pose f(x) =
J'ai d'abord montré qu'elle est définie sur R, continue, paire et 2-pi périodique.
On me demande ensuite de calculer f(0), f( ) , f(/2 )
C'est la que je n'y arrive pas, si quelqu'un peut me donner un coup de pouce, merci d'avance !

[Ben314]

Salut,
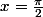
Ce n'est pas extrodinairement difficile, par exemple pour , tu as :

donc
La petite difficulté est de trouver la valeur des deux sommes.
La première se déduit des valeurs de et (racines carrées de l'unité)
La seconde de , , et (racines 4em de l'unité)

Bon courage...

[nico742]

Merci déjà pour le raisonnement.
Bon pour le cas x=0, on a f(0) = (/2)e si je ne me trompe pas ?
En revanche, je galère pour calculer ces sommes plus compliquées...

[Finrod]

essai d'écrire en serie entière, les termes pairs vont se téléscoper.

[Ben314]

Euhhhh, pour f(0), je trouverais plutôt 0 car
arcos(cos(nx0))=arcos(1)=0 !!!

Pour f(pi), c'est encore assez gentil, la seule série que tu as est sensée être "connue", (sinon ajoute/retranche les séries de exp(1) et de exp(-1))

La seule qui pose vraiment problème est celle des 1/(4k+2)! qu l'on peut obtenir en "tripatouillant" les séries de exp(1), exp(i), exp(-1) et exp(-i) [tripatouiller veut dire de les ajouter/soustraire et de les multiplier éventuellement par 1,-1,i,-i]

Je te laisse chercher un peu...

[nico742]

Oui pardon pour le f(0) j'étais allé vite.

Pour la somme je trouve qu'elle est égale à (e-e(-1)) , j'espère ne pas m'être planté , je vais me pencher sur la deuxième.

[nico742]

:marteau: :marteau:

J'espère que c'est pas censé être trouvable facilement...parce que je ne trouve pô :zen:

[Ben314]

Dans les séries de exp(1), exp(i), exp(-1), exp(-i), les coeffs au dessu du n! se répètent de 4 en 4, donc pour pas me faire ch.., j'écrit que les 4 premiers [entre crochet]
exp(1) =[ 1 1 1 1]
exp( i) =[ 1 i -1 -i]
exp(-1)=[ 1 -1 i -i ]
exp(-i) =[ 1 -i -1 i ]

Avec ces notations, par exemple la somme des 1/(2k+1)! correspond à
[0 1 0 1] est c'est bien 1/2(exp(1)-exp(-1))

La somme des 1/(4k+2)! correspond à [0 0 1 0] et, pour trouver son expression, on peut résoudre :
a[1 1 1 1] + b[1 i -1 -i] + c[1 -1 i -i ] + d[1 -i -1 i ] = [0 0 1 0]
en fait, comme par hasard, la matrice de ce système est une matrice de Vandermonde...