[resolu] Borne sup et plus grand élément

[Benk]

Bonjour à tous,

je suis en pcsi, et j'aurais une question à propos du chapitre sur les corps réels...

J'ai du mal à faire la différence entre "le plus grand élément de A", et "la borne supérieure de A"..

En effet, d'après la définition vu en cours, j'ai:

"a" plus grand élément ssi 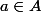et ,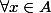

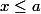
Borne Supérieure de A = Sup A = + petit des majorants de A

En effet, ce qui me fait douter sur la différence de ces deux définitions est le fait que le professeur ajoute:

Si A admet un plus grand élément "a0", alors Sup A existe et vaut "a0" .

[Ben314]

Bonsoir,
Le problème c'est que l'affirmation du prof. est (évidement) vraie, mais il aurait dû rajouter que la réciproque est fausse.
Par exemple l'intervalle [0,1[ de R admet une borne sup (qui est 1) mais pas de plus grand élément...

[Benk]

Bonsoir,
Le problème c'est que l'affirmation du prof. est (évidement) vraie, mais il aurait dû rajouter que la réciproque est fausse.
Par exemple l'intervalle [0,1[ de R admet une borne sup (qui est 1) mais pas de plus grand élément...

Comment me faire comprendre quelque chose en deux phrases.. merci, je vient de comprendre...

Bonne soirée à tous, et merci encore