Matrice diagonale et limites

[stma]

Bonjour,
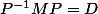
On me demande de calculer où D est une matrice diagonale.
Ensuite on me demande de calculer et sa limite quand n tend vers l'infini et

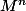
[Ben314]

Bonjour,
Si la matrice D est diagonale, le calcul de D^n est... trés simple.
Essaye par exemple avec une matrice 3x3 :


Si tu n'as jamais vu le résultat, montre le (par récurrence sur n)

Bon courage.

[stma]

Bonjour,
Si la matrice D est diagonale, le calcul de D^n est... trés simple.
Essaye par exemple avec une matrice 3x3 :


Si tu n'as jamais vu le résultat, montre le (par récurrence sur n)

Bon courage.

Finalement si je cherche , Soit je fais comme tu l'as décrit ou si je fais , suis je censé trouvé le même résultat ?
Car je ne trouve pas le même résultat... D'ailleurs sinon il n'y aurait plus besoin d'appliquer la formule.

[Ben314]

...si je fais , suis je censé trouvé le même résultat ?

La réponse est évidement oui !!!
Sauf que, dans ce type d'exo., les erreurs de calculs sont... trés fréquentes !!!
Vu la quantité de calculs nécéssaire au calcul des sous espaces propre (i.e. de la matrice P) puis au calcul de P^{-1}, quand on a le temps, je conseillerais fortement de vérifier que l'on a bien M=PDP^{-1}.
Si on n'a pas calculé P^{-1}, on peut quand même vérifier que MP=PD...

[stma]

je ne trouve pas la même chose :cry:
Pourtant P est bon car c'est la matrice des vecteurs propres de M qui est donnée dans l'énoncé sauf un que j'ai calculé !
P-1 je l'ai calculé, je l'ai vérifié également sous excel et on s'accorde sur la même chose.
P-1MP = D (là je trouve bien tous mes vecteurs propres).
Par contre P-1 D P n'est pas égal à M !

[stma]

La réponse est évidement oui !!!
Sauf que, dans ce type d'exo., les erreurs de calculs sont... trés fréquentes !!!
Vu la quantité de calculs nécéssaire au calcul des sous espaces propre (i.e. de la matrice P) puis au calcul de P^{-1}, quand on a le temps, je conseillerais fortement de vérifier que l'on a bien M=PDP^{-1}.
Si on n'a pas calculé P^{-1}, on peut quand même vérifier que MP=PD...

MP = PD, je trouve pareil
donc M = PDP-1

[stma]

je dois avoir faux sur ma matrice p

[miikou]

salut c'est PD^nP-1=M^n
tu peux donner les valeures propres de D ? a priori faudrait que leurs modules soient inferieurs a 1

[stma]

les valeurs propres sont bonnes et leurs sommes sont égales à 1 tout comme la trace de ma matrice M.
Je pense avoir tout juste jusqu'ici, je viens de faire le calcul de M^n.
D^n également.

[miikou]

jte crois ..
jdisais juste que pour esperer avoir convergance il faut que le module soit inferieur a 1

[stma]

jte crois ..
jdisais juste que pour esperer avoir convergance il faut que le module soit inferieur a 1

je viens de toute refaire et je te remercie de ton coup de main, pour l'instant tout est bon et tout roule :zen:

[Ben314]

(Re)salut,
Si j'ai par mégarde confondu M=PDP^-1 et M=P^-1DP, je m'en excuse platement...
Dans ce type de formule, tout dépent de qui on appelle P (ça c'est pour tenter de justifier que j'ai peut-être écrit une c... :zen: )