relis la réponse de Ben, son deuxième message.
Et
pis
ça suffit mathelot de le faire tourner autour du pot comme ça.
Dm pour demain
37 messages
- Page 2 sur 2 - 1, 2
par Sve@r » 13 Jan 2010, 18:45
DbbS a écrit:bon sa commence a m'enerver
Tu sais, la question initiale étant "comment peut-on regrouper ces objets en 2 catégories", il s'agit ici d'une question ouverte qui fait simplement appel à ton imagination et qui n'a pas de réponse attendue. On peut par exemple distinguer les objets qui ont des angles avec ceux qui n'en ont pas ; ou bien ceux qui ont un nombre d'angles pair et ceux qui ont un nombre impair ; ou bien ceux qui ont toutes leurs des surfaces planes et ceux qui ne les ont pas toutes ; ou bien ... bref à toi d'imaginer ce qui te parait le plus sensé. Comme ta dernière leçon parle de Pythagore et que Pythagore s'applique aux angles droits, tu peux essayer de voir par là...
par Ben314 » 13 Jan 2010, 18:47
Perso, je trouve ça franchement trés con comme question !!!
Ca me parrait aussi malin que le "complétez "logiquement" la suite de nombres suivantes" ou on peut répondre n'importe quoi en disant (par exemple) qu'on a pris un polynôme d'interpolation.
Y'en a beaucoup des questions comme ça dans les bouquins de collège ?
P.S. j'enlève le post dans 10 minutes (avant la fin de sa douche...)
EDIT2 : Trop tard...
EDIT : j'avais pas lu le post de svear.
Si c'est effectivement vu comme une "question ouverte" je retire ce que j'ai dit... (le p.b. c'est que pour un devoir MAISON, je suis pas sûr que les gamins voient que c'est "ouvert"...)
Ca me parrait aussi malin que le "complétez "logiquement" la suite de nombres suivantes" ou on peut répondre n'importe quoi en disant (par exemple) qu'on a pris un polynôme d'interpolation.
Y'en a beaucoup des questions comme ça dans les bouquins de collège ?
P.S. j'enlève le post dans 10 minutes (avant la fin de sa douche...)
EDIT2 : Trop tard...
EDIT : j'avais pas lu le post de svear.
Si c'est effectivement vu comme une "question ouverte" je retire ce que j'ai dit... (le p.b. c'est que pour un devoir MAISON, je suis pas sûr que les gamins voient que c'est "ouvert"...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par DbbS » 13 Jan 2010, 18:52
Oui merci c'est vraie que je voyer pas sa comme sa car moi aussi je trouvai la question vague :D merci
par Sve@r » 13 Jan 2010, 18:53
Ben314 a écrit: (le p.b. c'est que pour un devoir MAISON, je suis pas sûr que les gamins voient que c'est "ouvert"...)
Il y aura ceux qui voient de suite (ceux qui ont un esprit tourné aussi vers l'imaginatif) et ceux qui, trop tournés vers le cartésien, bloquent désespérément parce qu'ils n'ont pas assez de critère. C'est aussi une façon de faire un début d'orientation scolaire...
par Ben314 » 13 Jan 2010, 18:58
C'est pas faux du tout,
Et là où on voit que je suis trés con (ou trop formaté par le système) c'est que ma première réaction façe à un exercice de ce type est de trouver ça anormal alors que je sait que le système scolaire conduit à ce que, façe à une question du type "toto a deux bonbons dans la poche droite et trois dans la gauche. Quel est l'age de toto", il y a beaucoup plus d'enfant scolarisés qui répondent 5 ans (ou 6 ans) que parmi les non scolarisés...
Et là où on voit que je suis trés con (ou trop formaté par le système) c'est que ma première réaction façe à un exercice de ce type est de trouver ça anormal alors que je sait que le système scolaire conduit à ce que, façe à une question du type "toto a deux bonbons dans la poche droite et trois dans la gauche. Quel est l'age de toto", il y a beaucoup plus d'enfant scolarisés qui répondent 5 ans (ou 6 ans) que parmi les non scolarisés...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par DbbS » 13 Jan 2010, 19:03
Une pyramide a une surface plane ou pas car le haut non mais le bas oui qui l'emporte :D
par Sve@r » 13 Jan 2010, 19:10
DbbS a écrit:Une pyramide a une surface plane ou pas car le haut non mais le bas oui qui l'emporte
Une pyramide style Egypte possède 4 surfaces planes, les 3 premières étant montées sur la 4° appelée "base" de forme triangulaire
Une pyramide style Inca possède 5 surfaces planes, les 4 premières étant montées sur une 5° de forme carrée
par Sve@r » 13 Jan 2010, 19:14
DbbS a écrit:Donc cest une surface plane ou pas la pyaramide :d
Ta question n'a pas de sens. Une pyramide n'est pas une surface, c'est un volume.
J'ai parlé (suite au post de Ben314) d'objets ayant des surfaces planes, en opposition avec des objets ayant des surfaces non planes. Une pyramide n'a que des surfaces planes, alors qu'un cylindre possède une base plane et une colonne repliée sur elle-même (donc non plane). Et une sphère n'a qu'une seule surface non plane. Mais tous les objets en question sont des volumes.
et le nombre pi
par mathelot » 13 Jan 2010, 20:11
Bon,
je complète ma réponse: je pensais aux solides dont les aires des surfaces et les volumes étaient calculés avec le nombre
, nombre transcendant et les autres, ce type de problème,d'ordre algébrique, étant lié à la quadrature du cercle et la duplication du cube
catégorie 1 (avec)
sphère, cone, cylindre
catégorie 2 (sans)
prismes, pyramides,cube,dodécaèdre
l'aire et le volume du dodécaèdre étant calculés avec le nombre
irrationnel mais algébrique. ( n'est pas algébrique)
je complète ma réponse: je pensais aux solides dont les aires des surfaces et les volumes étaient calculés avec le nombre
catégorie 1 (avec
sphère, cone, cylindre
catégorie 2 (sans
prismes, pyramides,cube,dodécaèdre
l'aire et le volume du dodécaèdre étant calculés avec le nombre
irrationnel mais algébrique. (
par Sve@r » 13 Jan 2010, 20:50
mathelot a écrit:Bon,
je complète ma réponse: je pensais aux solides dont les aires des surfaces et les volumes étaient calculés avec le nombre
catégorie 1 (avec
sphère, cone, cylindre
catégorie 2 (sans
prismes, pyramides,cube,dodécaèdre
l'aire et le volume du dodécaèdre étant calculés avec le nombre
irrationnel mais algébrique. (
C'est aussi une façon (à laquelle je n'avais pas pensé) de départager chaque volume. Mais c'est peut-être un poil difficile pour le niveau collège (qui ne connaissent pas encore les formules de calcul de chaque volume) :zen:
par Ben314 » 13 Jan 2010, 21:52
Tient, tant qu'à faire de "papoter" :
Niveau math., y'a rien à dire, mais au niveau égyptologie, j'ai des doutes...Sve@r a écrit:Une pyramide style Egypte possède 4 surfaces planes, les 3 premières étant montées sur la 4° appelée "base" de forme triangulaire
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
du point de vue de l'IA
par mathelot » 13 Jan 2010, 22:55
re,
ce qui est troublant (confusant), c'est la présence simultanée dans la liste
de
cube + prisme rectangulaire
le prisme rectangulaire est nommé aussi parallèlipipède rectangle,
pavé droit ou cuboïde.
Du point de vue topologique et combinatoire (#A,#F,#S) et géométrie
différentielle, ce sont les mêmes objets, cube et prisme rectangulaire. Simplement, le cube rend le volume minimal dans la famille des prismes rectangulaires de surface identique.
La sphère est toute seule par le fait d'avoir une seule face et un nombre indéfini de sommet(s).
Pour les polyèdres convexes, on a la relation d'Euler
#F+#S-#A=2
pour le cube: 6+8-12=2
pour le dodécaèdre: 12+20-30=2
pour la pyramide: (n+1)+(n+1)-2n=2
Examinons un patron de cylindre, constitué d'un rectangle
et deux disques:
#F=3; #A=6 chaque cercle étant considéré comme une arête.
On colle deux bords du rectangle, ce qui diminue le nombre d'arêtes de 1
et chaque cercle avec un côté de rectangle, ce qui diminue le nombre d'arêtes de 2.
d'où, pour le cylindre: #F=3;#A=3;#S=2
les sommets du cylindre sont les intersections d'arêtes. or le graphe des arêtes est constitué de deux cercles reliés par un segment.
d'où #F=3;#A=3;#S=2
topologiquement, une sphère est la réunion d'un point (pole Nord)
et d'un plan (cf projection stéréographique)
d'où #F=1;#S=1;#A=0 puisque les ar^tes sont des intersections
de deux faces distinctes.
Comme on disposait de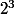
=8 solides, on aurait dû définir,pour l'exercice, trois catégories
et un arbre binaire. Mais cette classification est improbable à cause
de la présence simultanée du cube et cuboïde que l'on arrivera pas à distinguer (ou très difficilement)
ce qui est troublant (confusant), c'est la présence simultanée dans la liste
de
cube + prisme rectangulaire
le prisme rectangulaire est nommé aussi parallèlipipède rectangle,
pavé droit ou cuboïde.
Du point de vue topologique et combinatoire (#A,#F,#S) et géométrie
différentielle, ce sont les mêmes objets, cube et prisme rectangulaire. Simplement, le cube rend le volume minimal dans la famille des prismes rectangulaires de surface identique.
La sphère est toute seule par le fait d'avoir une seule face et un nombre indéfini de sommet(s).
Pour les polyèdres convexes, on a la relation d'Euler
#F+#S-#A=2
pour le cube: 6+8-12=2
pour le dodécaèdre: 12+20-30=2
pour la pyramide: (n+1)+(n+1)-2n=2
Examinons un patron de cylindre, constitué d'un rectangle
et deux disques:
#F=3; #A=6 chaque cercle étant considéré comme une arête.
On colle deux bords du rectangle, ce qui diminue le nombre d'arêtes de 1
et chaque cercle avec un côté de rectangle, ce qui diminue le nombre d'arêtes de 2.
d'où, pour le cylindre: #F=3;#A=3;#S=2
les sommets du cylindre sont les intersections d'arêtes. or le graphe des arêtes est constitué de deux cercles reliés par un segment.
d'où #F=3;#A=3;#S=2
topologiquement, une sphère est la réunion d'un point (pole Nord)
et d'un plan (cf projection stéréographique)
d'où #F=1;#S=1;#A=0 puisque les ar^tes sont des intersections
de deux faces distinctes.
Comme on disposait de
et un arbre binaire. Mais cette classification est improbable à cause
de la présence simultanée du cube et cuboïde que l'on arrivera pas à distinguer (ou très difficilement)
37 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :