Calcul de dérivée (rapide)

[fifig10]

Bonjour,

J'aimerais une vérification.
On me demande de trouver f'(x) pour f(x)=(.
D=R-{0}
J'ai utilisé le théorème lorsque f(x)=u(x) , f'(x)=n*u'(x)* et j'ai trouvé 6.
Je me demande aussi si ce théorème ne découle pas de f'(x)=af'(ax+b).

Merci d'avance

[lysli]

Hmm, tu dois aussi dériver

J'ai utilisé le théorème lorsque f(x)=u(x) , f'(x)=n*u'(x)*

Regarde bien ce que tu as écrit ici et ce que tu as fait après

[Sve@r]

J'ai utilisé le théorème lorsque f(x)=u(x) , f'(x)=n*u'(x)* et j'ai trouvé 6.

T'es sûr ? Si on pose , alors donc je suis étonné que la fraction n'apparaisse pas dans ton, résultat...

[fifig10]

u'(x)=1/(2)
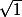
Donc f'(x)=3*[1/(2 )]*+1 ?
Je pensais que u(x) représentait la fonction cube.

[Ben314]

Salut,
Dans ton "premier essai", tu avais "oublié" le et cette fois, c'est le que tu oublie...

Essaye encore... :happy2:

[fifig10]

u'(x)=1/(2)
u(x) = ()
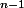
Oui merci.
et cette fois ci f'(x)=3*[1/(2)]*() ?

[lysli]

et cette fois ci f'(x)=3*[1/(2)]*() ?

y a un problème n'est pas égal
u(x)= ?

[lysli]

u'(x)=1/(2)
= ()

C'et bon

et cette fois ci f'(x)=3*[1/(2)]*

Non

[fifig10]

Ah oui, petite erreur !
f'(x)=3**