Calcul

[marinahaha]

Bonjour, J'ai un petit problème enfaite j'ai déjà fait la moitié de l'exercice mais au bout d'un moment dans mon calcul j'arrive à ça:



J'ai réussi à mettre sur le même dénominateur, mais je reste bloquer là... :triste:
Si quelqu'un pourrais m'aider à résoudre, en tout cas me mettre sur la voie...

[olivier azerty]

Bonsoir
Je ne comprend pas ton problème... puisque si tu a tous mis sur le même dénominateur tu as:
(2x - 4 - 3x + 1) / (x² - 4)
Après c'est simple ! Ne vois-tu pas la possibilité de le réduire encore un peu ?

[benoit16]

ATTENTION il y a une erreur de signe

[marinahaha]

euh...je vais remettre l'énonce et tout ce que j'ai déjà fait :

Résoudre dans R l'équation : 2/(x+2)=(3x+1)/(x²-4)

Donc pour prouver l'égalité j'ai décider de résoudre l'équation, s'il sont vraiment égaux je devrais me retrouver avec 0=0
(exemple: 6/2=3 , 6/2 -3=0 , 3-3=0 , 0=0 )
C'est comme ça que le professeur a fait au tableau pour un exercice.

Donc j'ai fait :





Et après je ne sais plus comment faire...


P.s: Désolé de toute ces parenthèses...

[Ericovitchi]

le plus simple à partir de 2/(x+2)=(3x+1)/(x²-4)

c'est de faire le produit en croix

2(x²-4)=(3x+1)(x+2) de ramener tout d'un coté:

2(x²-4)-(3x+1)(x+2)=0 puis mettre (x+2) en facteur en utilisant le fait que x²-4 est un a²-b²

[Sa Majesté]

le plus simple à partir de 2/(x+2)=(3x+1)/(x²-4)

c'est de faire le produit en croix

2(x²-4)=(3x+1)(x+2) de ramener tout d'un coté:

2(x²-4)-(3x+1)(x+2)=0 puis mettre (x+2) en facteur en utilisant le fait que x²-4 est un a²-b²

Je ne suis pas de cet avis car en faisant comme ça, tu obtiens (x+2) en facteur et donc tu introduis une fausse solution (x=-2)

La façon de faire de marinahaha me semble meilleure (en tout cas moins risquée)

[marinahaha]

Ah ! oui je viens de comprendre, je pense que je vais faire comme ça !
Donc après avoir fait le produit en croix et avoir tout mis a gauche, j'ai donc :

2[ (x+2) (x-2) ]-(x+2) (3x+1) = 0

Et là pour faire la forme a(b-c)
Es-ce que je peux faire :
(x+2) [(2(x-2)) (3x+1)] = 0 ?? :hum:

[marinahaha]

Je ne suis pas de cet avis car en faisant comme ça, tu obtiens (x+2) en facteur et donc tu introduis une fausse solution (x=-2)

La façon de faire de marinahaha me semble meilleure (en tout cas moins risquée)

ah...euh...beh je sais plus quoi faire maintenant ! x)
Dans tout les cas de nimporte qu'elle façon je passe je me bloque toute seule :triste:

[Sa Majesté]

A partir de là




Là ça devrait aller non ?

[marinahaha]

A partir de là




Là ça devrait aller non ?

Oui, mais avec ça en fin on ne peut pas arriver à 0=0 car on ne peux pas le réduire ? , il me faut prouver qu'ils sont égaux pour la suite.

[Sa Majesté]

Tu cherches à résoudre une équation, c'est-à-dire à trouver toutes les valeurs de x telles que

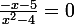
[marinahaha]

Tu cherches à résoudre une équation, c'est-à-dire à trouver toutes les valeurs de x telles que

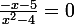
Non je ne veux pas savoir combien fait x à la fin enfaite j'ai ça comme enoncé:

Résoudre l'équation 2/(x+2) = (3x+1)/ (x²-4)

Il faut donc que je prouve l'égalité, j'ai trois solutions :
-partir de 2/(x+2) et retombé sur (3x+1)/ (x²-4) ;
-partir de (3x+1) / (x²-4) et retombé sur 2/(x+2) ;
-calculer 2/(x+2) = (3x+1)/ (x²-4) et trouver à la fin 0=0

J'ai commencer a faire la 3ème méthode.
j'ai essayer ça :





Après là je suis bloqué...

[Sa Majesté]

Non je ne veux pas savoir combien fait x à la fin enfaite j'ai ça comme enoncé:

Résoudre l'équation 2/(x+2) = (3x+1)/ (x²-4)

Il faut donc que je prouve l'égalité

Non justement ! C'est ce que j'essaie de te faire comprendre
Apparemment tu n'as pas compris ce qu'est une équation

Si tu cherches à montrer que pour tout x
2/(x+2) = (3x+1)/ (x²-4)
alors bon courage !
Il n'y a qu'à prendre x=0 (entre autres) pour voir que ça ne marche pas

Je me répète : résoudre l'équation c'est trouver les valeurs de x telles que
2/(x+2) = (3x+1)/ (x²-4)

[marinahaha]

Non justement ! C'est ce que j'essaie de te faire comprendre
Apparemment tu n'as pas compris ce qu'est une équation

Si tu cherches à montrer que pour tout x
2/(x+2) = (3x+1)/ (x²-4)
alors bon courage !
Il n'y a qu'à prendre x=0 (entre autres) pour voir que ça ne marche pas

Je me répète : résoudre l'équation c'est trouver les valeurs de x telles que
2/(x+2) = (3x+1)/ (x²-4)

euh...à vrai dire je ne comprend pas du tout ce que vous voulez dire :/

[Sa Majesté]

Prenons un exemple plus simple
x+2=0 c'est une équation, c'est-à-dire que l'égalité n'est pas vraie pour tous les x réels mais seulement pour certaines valeurs
Chercher ces valeurs, c'est résoudre l'équation
Dans l'exemple ci-dessus, il n'y en a qu'une, c'est x=-2

Pour ton cas c'est pareil
2/(x+2) = (3x+1)/ (x²-4) c'est une équation
Il faut que tu trouves les valeurs de x qui font que l'égalité est vraie
Par exemple x=0 ne marche pas car à gauche tu as 1 et à droite tu as -1/4