Tangente
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Gagnantdu06
- Membre Relatif
- Messages: 224
- Enregistré le: 26 Déc 2008, 15:47
-
 par Gagnantdu06 » 06 Jan 2010, 13:46
par Gagnantdu06 » 06 Jan 2010, 13:46
Bonjour, je suis bloqué à la fin de mon exercice (le début de l'exercice n'aide pas pour cette question donc je ne le marque pas):
g est la fonction définie sur

par f(x) =

C est la courbe représentant g dans un repère.
a)T est la tangente à C en un points d'abscisse
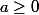
.
Déterminer a pour que T passe par l'origine du repère. Donner une équation de cette tangente.
-
oscar
- Membre Légendaire
- Messages: 10024
- Enregistré le: 17 Fév 2007, 20:58
-
 par oscar » 06 Jan 2010, 14:37
par oscar » 06 Jan 2010, 14:37
T : y =f'(a) (x-a) + f(a)=
T passe par O origine du repère=> calcule T
-
Gagnantdu06
- Membre Relatif
- Messages: 224
- Enregistré le: 26 Déc 2008, 15:47
-
 par Gagnantdu06 » 06 Jan 2010, 14:41
par Gagnantdu06 » 06 Jan 2010, 14:41
il faut que je calcule la dérivée de a pour donner l'image de f'(a)?
-
Gagnantdu06
- Membre Relatif
- Messages: 224
- Enregistré le: 26 Déc 2008, 15:47
-
 par Gagnantdu06 » 06 Jan 2010, 14:57
par Gagnantdu06 » 06 Jan 2010, 14:57
Je trouve
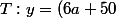(x-a)+3x^2+50x+2700)
Comment trouver a?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 06 Jan 2010, 15:12
par Ben314 » 06 Jan 2010, 15:12
Gagnantdu06 a écrit:Je trouve
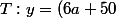(x-a)+3x^2+50x+2700)
C'est "presque" ça, mais pas tout à fait (il y a une erreur entre certains 'x' et 'a')
Ensuite, tu réfléchi pour voir à quelle condition une telle droite passe par le point O de coordonnées x=0, y=0...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Gagnantdu06
- Membre Relatif
- Messages: 224
- Enregistré le: 26 Déc 2008, 15:47
-
 par Gagnantdu06 » 06 Jan 2010, 15:36
par Gagnantdu06 » 06 Jan 2010, 15:36
Oué désolé erreur d'inattention en tapant Je trouve plutôt
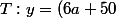(x-a)+3a^2+50a+2700)
ce qui donne donc

Mais après je vois pas comment faire ...
Je pensais à résoudre une équation du type =0 mais je pense que c'est trop compliqué donc ce n'est pas ce qu'il faut faire.
-
Gagnantdu06
- Membre Relatif
- Messages: 224
- Enregistré le: 26 Déc 2008, 15:47
-
 par Gagnantdu06 » 06 Jan 2010, 16:22
par Gagnantdu06 » 06 Jan 2010, 16:22
Personne ne peut me venir en aide? car c'est pour demain et me manque juste ça.
-
Gagnantdu06
- Membre Relatif
- Messages: 224
- Enregistré le: 26 Déc 2008, 15:47
-
 par Gagnantdu06 » 06 Jan 2010, 17:56
par Gagnantdu06 » 06 Jan 2010, 17:56
J'ai trouvé comme le point (0;0) appartient à T on remplace x et y par 0 et cela donne une équation en a c'est cela?
-
Teacher
- Membre Rationnel
- Messages: 732
- Enregistré le: 12 Nov 2007, 20:03
-
 par Teacher » 06 Jan 2010, 18:04
par Teacher » 06 Jan 2010, 18:04
Il faut que 0 = f '(a) (0-a) + f(a) avec a réel positif

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 06 Jan 2010, 18:08
par Ben314 » 06 Jan 2010, 18:08
Gagnantdu06 a écrit:J'ai trouvé comme le point (0;0) appartient à T on remplace x et y par 0 et cela donne une équation en a c'est cela?
Oui, c'est bien ça.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Gagnantdu06
- Membre Relatif
- Messages: 224
- Enregistré le: 26 Déc 2008, 15:47
-
 par Gagnantdu06 » 06 Jan 2010, 20:28
par Gagnantdu06 » 06 Jan 2010, 20:28

Donc je remplace y et x par 0 dans l'équation
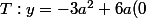+50(0)+2700)
alors est si cela donne:
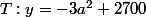
ou

-
Teacher
- Membre Rationnel
- Messages: 732
- Enregistré le: 12 Nov 2007, 20:03
-
 par Teacher » 06 Jan 2010, 20:45
par Teacher » 06 Jan 2010, 20:45
a=30 et y=230x
-
Teacher
- Membre Rationnel
- Messages: 732
- Enregistré le: 12 Nov 2007, 20:03
-
 par Teacher » 06 Jan 2010, 20:50
par Teacher » 06 Jan 2010, 20:50
Tu as T: y = (6 a + 50) (x - a) + 3 a² + 50 a + 2700
y = (6 a + 50) (x - a) + 3 a² + 50 a + 2700 passant par (0;0)
0 = (6 a + 50) (0 - a) + 3 a² + 50 a + 2700
0 = -a(6a+50)+3a²+50a+2700
-6a²-50a+3a²+50a+2700=0
-3a²+2700=0
On a donc deux solution en calculant delta: -30 et 30
Comme a doit être positif ou nul il reste plus que a = 30
Tu recalcules l'équation de ta tangente pour a=30 et tu trouves 230x:
y = (6X30 + 50) (x - 30) + 3 (30)² + 50X30 + 2700
y = 230x
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités