Module et argument
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Shigeaki
- Membre Naturel
- Messages: 20
- Enregistré le: 02 Jan 2010, 10:09
-
 par Shigeaki » 03 Jan 2010, 15:16
par Shigeaki » 03 Jan 2010, 15:16
Bonjour tout le monde
il faut de je détermine le module et un argument de
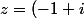( -sqrt{2} + i sqrt{2})^3)
pour le module, je trouve

Mais je ne vois pas comment calculer l'argument
Même chose pour
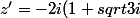^6)
Pour le module, je trouve 128, mais je ne vois pas comment trouver l'argument.
Merci d'avance

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 03 Jan 2010, 15:21
par Ericovitchi » 03 Jan 2010, 15:21
Tu l'as développé ? on trouve

effectivement. C'est un nombre réel donc l'argument est nul.
Et l'autre tu l'as développé ? on trouve un nombre imaginaire pur donc son argument est facile à trouver.
-
Shigeaki
- Membre Naturel
- Messages: 20
- Enregistré le: 02 Jan 2010, 10:09
-
 par Shigeaki » 03 Jan 2010, 15:28
par Shigeaki » 03 Jan 2010, 15:28
tu es sur de toi pour -

, car moi je trouve

et je croyais qu'un module êtant une distance, il était toujours positif.
-
Shigeaki
- Membre Naturel
- Messages: 20
- Enregistré le: 02 Jan 2010, 10:09
-
 par Shigeaki » 03 Jan 2010, 15:31
par Shigeaki » 03 Jan 2010, 15:31
Oups, j'avais fait une erreur de calcul, c'est pour ça que je trouvais des choses improbables... Ca va mieu maintenant
Merci

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 03 Jan 2010, 15:34
par Ericovitchi » 03 Jan 2010, 15:34
tu as calculé le module mais moi j'ai calculé directement le nombre complexe. Le module de

c'est effectivement

.
Si tu ne veux pas tout développer, tu as un moyen élégant. Tu considère que z est le produit de (-1 + i ) par ( -sqrt{2} + i sqrt{2})^3 donc de la forme u.w
Tu calcules le module et l'argument des deux et tu utilises les formules
|uw|=|u||w| et arg (uw)=arg(u)+arg(w)
pareil pour z' =
^6)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 86 invités