Bonjour,
Je me pose deux questions:
Comment montrer que pour une variable aléatoire X:
E(X²)>= (E(abs(X)))²
J'ai essayé avec l'inégalité de Jensen mais n'aboutis pas. Cette dernière me permets d'écrire:
(EX)²<=E(X²) et que abs(EX)<=E(abs(X)) et de plus on a (EX)²=(abs(EX))²
Mais ceci ne me permets de conclure....
Ma deuxième question concerne le calcul de l'ésperance de la variable carrée d'une loi normale Y -> N(0,1)
E(Y²)??
Le calcul se ramène à l'intégrale ( a un coéfficient près ) int(x²*exp(-x²/2),x=-infinity..+infinity)...
et je ne vois pas comment continuer le calcul...
Merci d'avance de vos réponses
Calculs d'éspérance
10 messages
- Page 1 sur 1
Louise2607 a écrit:Bonjour,
Je me pose deux questions:
Comment montrer que pour une variable aléatoire X:
E(X²)>= (E(abs(X)))²
J'ai essayé avec l'inégalité de Jensen mais n'aboutis pas. Cette dernière me permets d'écrire:
(EX)² N(0,1)
E(Y²)??
Le calcul se ramène à l'intégrale ( a un coéfficient près ) int(x²*exp(-x²/2),x=-infinity..+infinity)...
et je ne vois pas comment continuer le calcul...
Merci d'avance de vos réponses
pour la 2éme question tu as la variance et l'espérance de la variable Y et de plus tu as V(X)=E(X²)-E²(X) donc voilà tout est réglé !!
salut,
pour l'esperance
)
On a deux manières. La premiere avec la variance :
 = E(X^2) - E^2(X))
or si suit
suit ) on a
on a =0) et
et  = 1^2)
du coup
 = var(X) + E^2(X) = 1)
La deuxieme methode c'est en utilisant la composition :
) = \int f(x)P_X(x)dx)
avec la densité de
la densité de 
dans notre cas, on pose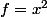 et on a
et on a 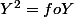
cqui donne ton integrale

i suffit de faire une IPP
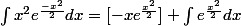
Entre crochet sfait 0 et l'autre integrale, c'est la densité d'une loi normale sur R et ca vaut 1 par definition(a la constante pres que t'as virée)!
sauf erreur
pour l'esperance
On a deux manières. La premiere avec la variance :
or si
du coup
La deuxieme methode c'est en utilisant la composition :
avec
dans notre cas, on pose
cqui donne ton integrale
i suffit de faire une IPP
Entre crochet sfait 0 et l'autre integrale, c'est la densité d'une loi normale sur R et ca vaut 1 par definition(a la constante pres que t'as virée)!
sauf erreur
la vie est une fête 
Louise2607 a écrit:Je suis désolé...mais je ne vois pas en quoi l'inégalité à montrer est évidente, même en utilisant Cauchy Schwarz?
tu poses Z=aX-Y tu calcules E(Z²) c'est un trinôme en a il a lieu si le discriminant est négatif ou égale à 0 puisque E(Z²) est positif donc tu en déduis l'inégalité que je t'ai proposée après pour en déduire la tienne c'est presque évident essaies de conclure !!
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 20 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
