Nature d'une série

par **hamdo** » 01 Jan 2010, 17:11

Salut tout le monde
Je cherche la nature de la série de terme générale

Merci d'avance

par **girdav** » 01 Jan 2010, 17:19

Salut.
Passe à l'exponentielle et cherche du côté de la comparaison série-intégrale.

par **hamdo** » 01 Jan 2010, 17:30

Merci girdav pour ta réponce,
peut-on prouver la convergence sans passer par cette comparaison?

par **girdav** » 01 Jan 2010, 17:39

Oui, en montrant qu'il existe un rang à partir duquel, par exemple,

.

par **hamdo** » 01 Jan 2010, 18:52

Merci infiniment girdav

par **bend** » 01 Jan 2010, 18:58

sion remarque que ; (1/2) ^ racine(n) inferieur (1/2) ^n qui converge

par **girdav** » 01 Jan 2010, 19:12

Attention, on a

donc

car

donc l'inégalité est dans l'autre sens.

par **yos** » 01 Jan 2010, 21:17

Autre méthode :

partant de

(pour n>100 disons), on obtient

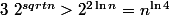
d'où le résultat par Riemann puisque