Bonsoir à tous, j'ai un soucis pour résoudre un exo:
Je dois étudier la série de terme général fn = 1/sh(nx) avec n entier naturel.
Je trouve le domaine de définition qui est R privé de 0.
Ensuite j'étudie la convergence simple, en utilisant les équivalent sur sh notamment je parviens à montrer qu'elle converge simplement.
Mais je bloque ensuite pour étudier la convergence uniforme.
Si quelqu'un peut me mettre sur la piste...merci d'avance !
Série de fonction
5 messages
- Page 1 sur 1
Ah oui, exact, donc on doit se contenter de la convergence uniforme. Néanmoins, même si ce n'est pas le but de la question on a, j'espère ne pas dire de bêtise cette fois, convergence normale sur tout ensemble de la forme  avec
avec  . Même si ceci ne permet en rien de conclure à la convergence uniforme sur
. Même si ceci ne permet en rien de conclure à la convergence uniforme sur 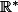 .
.
Je me demande si on peut calculer explicitement les sommes partielles.
Je me demande si on peut calculer explicitement les sommes partielles.
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
